Il DAC è l'acronimo di Convertitore Digitale Analogico.
In elettronica il DAC può essere realizzato in diversi modi.
Noi nell'esempio seguente lo realizzeremo con un Amplificatore operazionale in configurazione sommatore invertente, o con resistenze pesate.
Video sul DAC a resistenze pesate
Slides del DAC a resistenze pesate
Schema funzionale del DAC
Esperienza del DAC a resistenze pesate realizzata in laboratorio.
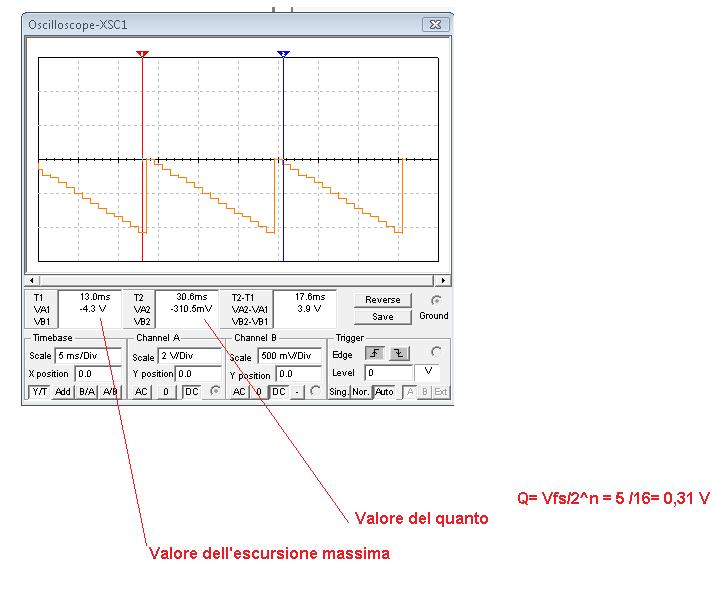
Gradinata invertente vista all'oscilloscopio
Teoria del DAC con resistenze pesate
Il DAC (Digital Analog Converter) è un convertitore digitale analogico.
Esso può essere realizzato con un amplificatore operazionale in configurazione sommatore invertente, o con resistenze pesate.
Ogni bit di ingresso a partire dall'LSB ( o cifra meno significativa) fino alla MSB ( cifra piu' significativa) contribuira' con il suo peso.
In questo caso noi realizzeremo:
il bit meno significativo dato dal rapporto tra R1/R5= 1KOhm/16K Ohm= 1/16 indicato con l'ingresso A,
e il bit piu' significativo dato dal rapporto tra R1/R2 = 1K Ohm/ 2,2K Ohm =1/2,2 indicato con l'ingresso D.
Quindi avremo :
bit A peso 1/16
bit B peso 1/8,2
bit C peso 1/4,7
bit D peso 1/ 2,2
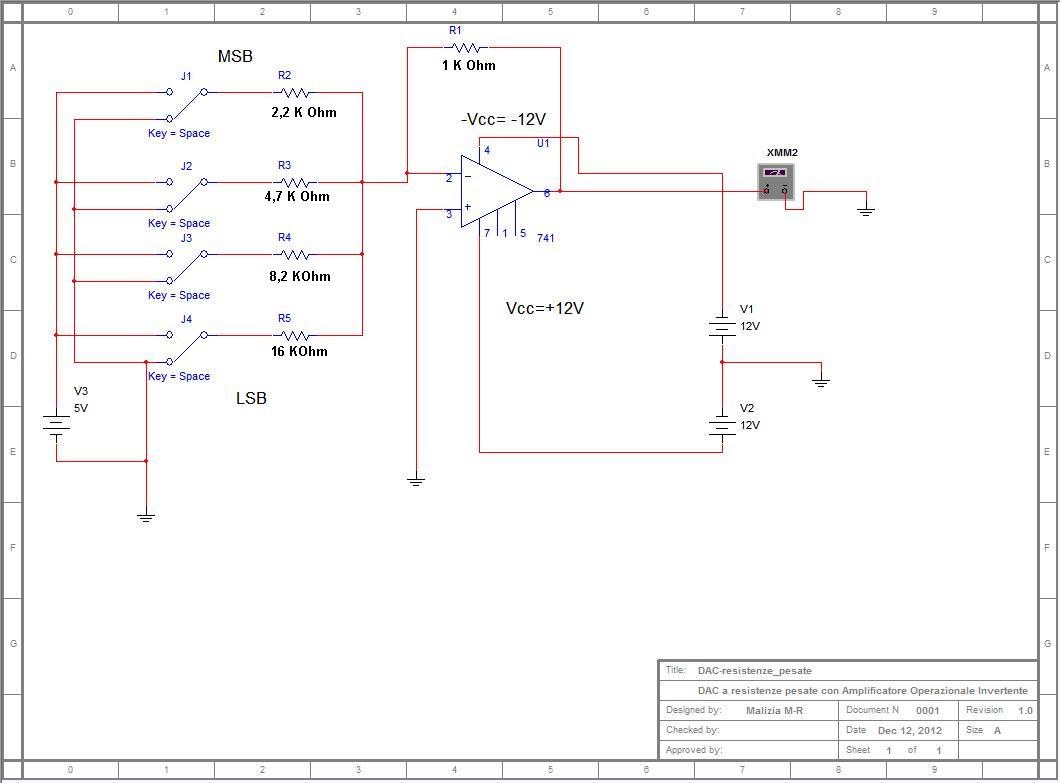
Schema elettrico del DAC a resistenze pesate
Il convertitore Digitale Analogico con resistenze pesate visualizza in uscita la tensione corrispondente ai bit selezionati di ingresso. La tensione di uscita per il principio di sovrapposizione degli effetti sarà in generale:
Vout(max) = -R1[( 1/R2) vi1 + (1/R3) vi2+ (1/R4) vi3 + ( 1/ R5) vi4]
Questo vuol dire che essendo R1 costante, anche gli altri coefficienti saranno costanti e contribuiranno alla tensione di uscita con il loro peso.
Valori pratici
Calcoliamo quindi questi pesi degli ingressi.
D= 1K Ohm / 2,2K Ohm = 0,454 ( cifra MSB o cifra più significativa)
C= 1K Ohm/ 4,7 K Ohm =0,213
B= 1K Ohm / 8,2 K Ohm =0,122
A= 1K Ohm / 16 K Ohm = 0, 0625 ( cifra LSB o cifra meno significativa).
sostituendo questi pesi la nostra tensione di uscita può anche essere scritta come:
Vout= - ( D vi 1 + C vi2 + B vi 3 + A vi4)
Essendo, nel nostro caso VFS( tensione di fondo scala o tensione di riferimento)
VFS=vi1=vi2=vi3=vi4= 5Volt
Vout= - (D+C+B+A)*VFS
Se abbiamo tutti gli ingressi a '1' logico, cioè collegati a VFS = 5Volt vuol dire che stiamo dando in ingresso il numero 15 decimale.
Sostituendo i valori pratici delle resistenze si ha:
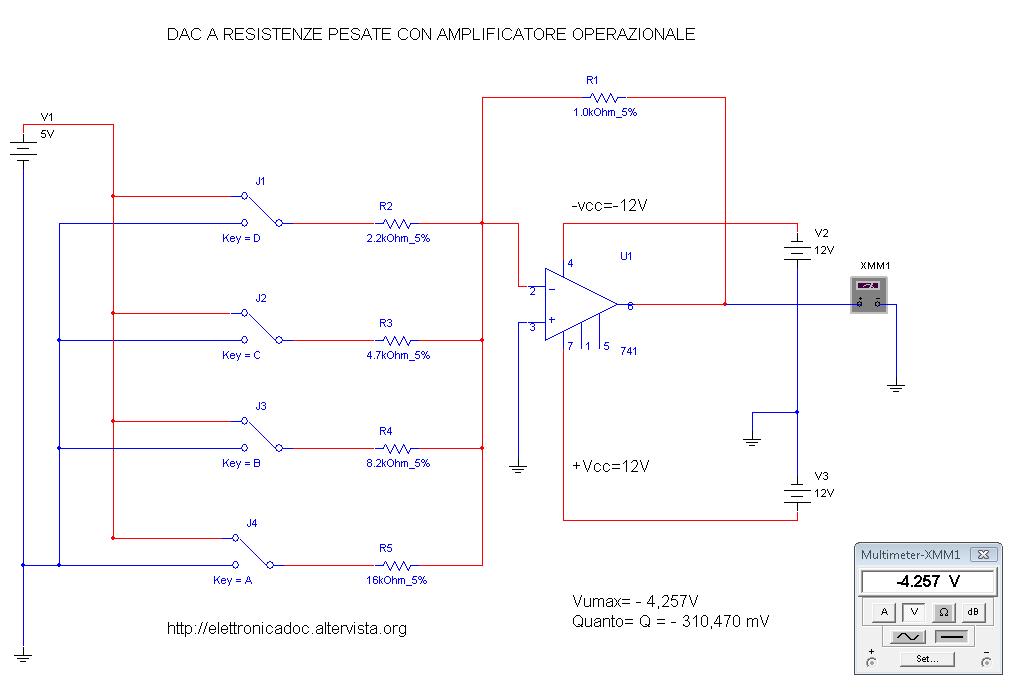
Vout (max)= - (D+C+B+A)*VFS= -( 0,454+0,213+ 0,122+0,0625) *5 = - 0,8515 *5= 4,2575
Valore pratico
Vout(max)= - 4,2575 Volt
Valori teorici
Questo valore è un pò diverso di quello che ci aspettavamo, in quanto con le resistenze pratiche i bit sono circa uguali a quelli teorici:
bit A peso 1/16 uguale 0,0625
bit B peso 1/8,2 cira uguale a quello teorico 1/8 = 0,125
bit C peso 1/4,7 circa uguale a quello teorico 1/4 =0,25
bit D peso 1/ 2,2 circa uguale a quello teorico 1/2 =0,5
Se nei nostri conti sostituivavamo i valori teorici si aveva:
Vout(max) = - ( 1/16 + 1/8 +1/4 +1/2 ) *5 Volt= - 0,9375*5= - 4,6875 Volt
Valore teorico
Vout (max)= - 4,6875 Volt
Formula generale del DAC: considerazioni teoriche
In teoria si ha:
Q = VFS/2^n
Se i bit sono 4 come nel nostro caso:
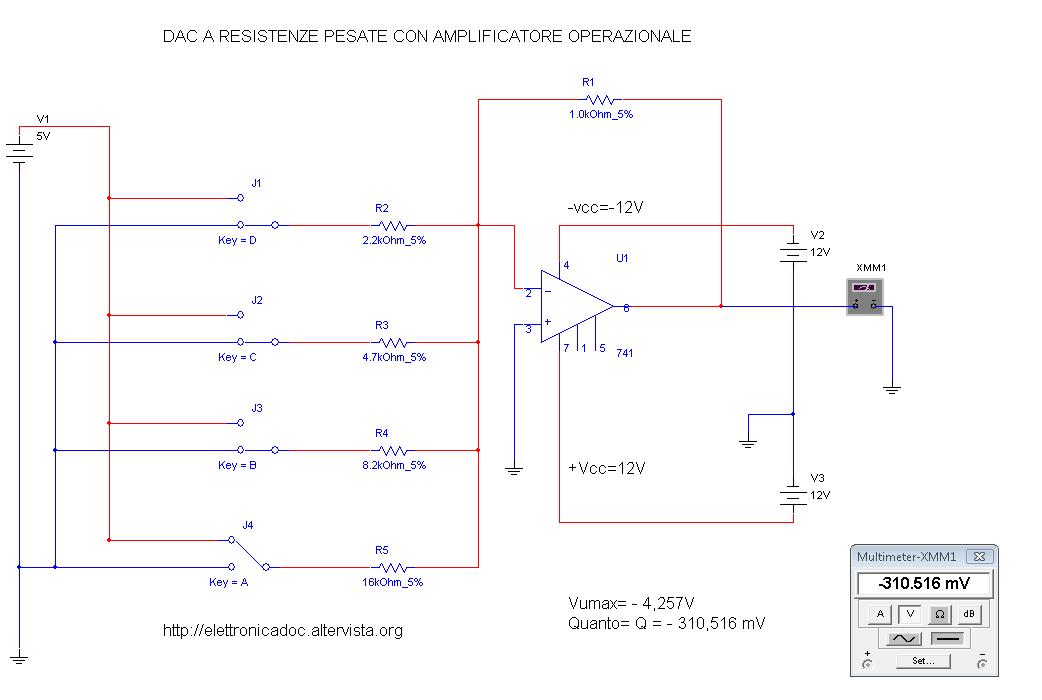
Q= 5/2^4 = 5/16 =0,3125 Volt
Q=0,3125 Volt
Vout = N(decimale)*Q
Vout(max)=(1/16+1/8+1/4+1/2)* VFS= ( 0,0625 + 0,125 +0,25 + 0,5)* 5 Volt = 4,6875 Volt
Vout(max)= VFS - Q = 5 - 0,13125 = 4,6875 Volt
Nel nostro caso essendo il sommatore invertente, bisogna considerare il segno meno della Vout.
Se il numero decimale N(decimale) = 15 si avrà in uscita:
Vout(max)= - N(decimale)*Q= - 15*0,3125 = - 4,6875 V
e ciò è equivalente al valore
Vout(max) = - (VFS - Q) = - ( 5 - 0,3125) Volt = - 4,6875 Volt
Calcoliamo Vout (max)
Calcoliamo il quanto: cifra LSB
DAC a resistenze pesate con contatore esadecimale in ingresso
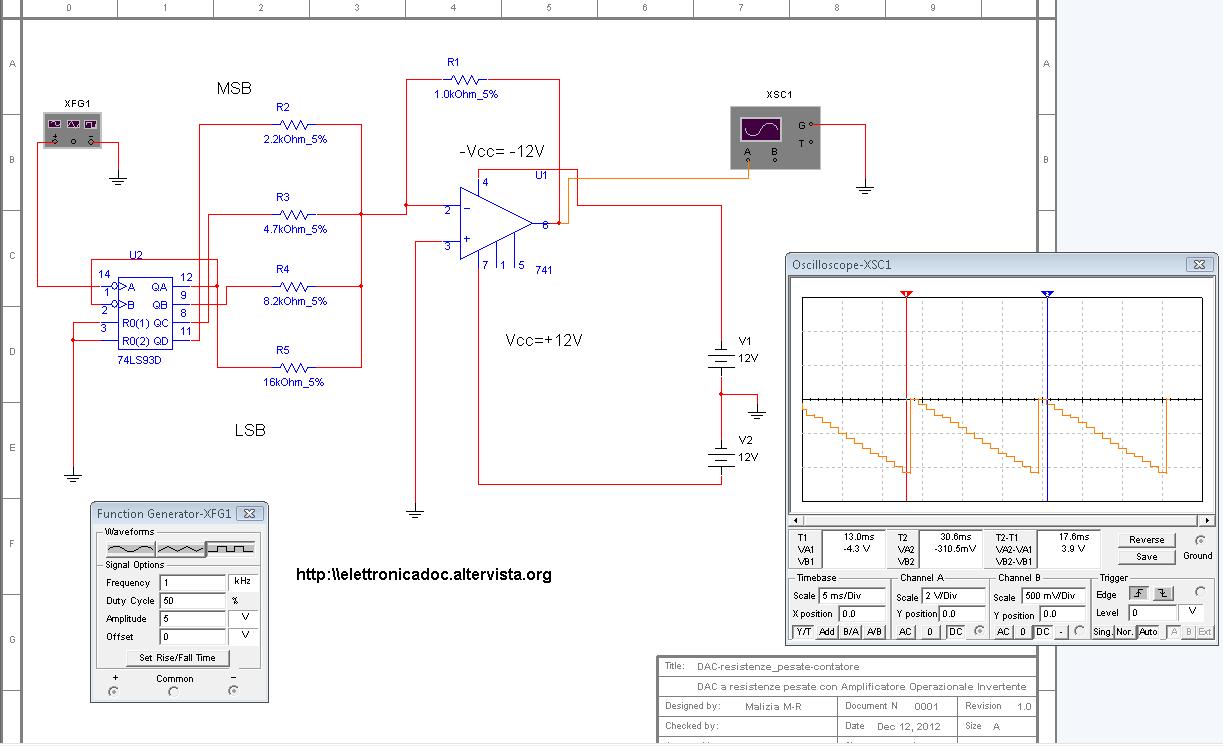
Guardiamo adesso lo schema elettrico del DAC a resistenze pesate in cui abbiamo aggiunto il contatore esadecimale 7493 per poter visualizzare le 16 combinazioni attraverso la simulazione con il Multisim.
Visualizzazione della gradinata con l'oscilloscopio
DAC con resistenze pesate con contatore 7490
E' possibile vedere il funzionamento del DAC a resistenze pesate sostituendo al contatore 7493 il contatore 7490. In quest'ultimo caso però avremo una escursione massima della gradinata inferiore e un numero di gradini uguale a 9 anziche 16. Questo perchè il contatore 7490, pur essendo pin compatibile, è un contatore decadico cioè conta da zero a nove.
La simulazione con il multisim dà in questo caso la seguente figura.
Pilotiamo il nostro convertitore Analogico Digitale in modo automatico con un contatore esadecimale, al cui ingresso di clocK CKA inviamo un'onda quadra alla frequenza di 1 K Hz.
Nel nostro esempio abbiamo utilizzato un contatore esadecimale 7493.
Le uscita Qa, QB, Qc, Qd del contatore sono state collegate agli ingressi corrispontenti del sommatore invertente .
Collegando l'uscita dell' amplificatore operazionale un oscilloscopio, potremo visualizzare sull'oscilloscopio la nostra gradinata decrescente.
Si avranno quindi 16 gradini di tensione, scansionati dalla frequenza del clocK fino ad arrivare alla tensione massima dell' ADC corrispondente al suo valore massimo.
In questo caso il quanto Q sarà sempre dato dal DAC a resistenze pesate
Q= 5/2^n=5/16=0,3125
ma l'escursione massima sarà dovuta a 10 gradini cioè
Vumax= - (10*Q-Q=9*Q) = - 9*0,3125 V= - 2,81 V.
Il segno meno è dovuto al fatto che la gradinata è invertente.