Diagrammi di Bode
I diagrammi di Bode sono delle rappresentazioni grafiche della funzione G(s).
Esistono due tipi di rappresentazione grafiche:
1) Diagramma del modulo in decibel al variare di w o della frequenza
2) Diagramma della fase al variare di w o della frequenza.
Il diagramma del modulo di G(s) in decibel cioè |G(s)| dB e il diagramma della fase di G(s) al variare di w o della frequenza sono dei grafici in scala semilogaritmica.
Nel diagramma del modulo sulle ascisse mettiamo i logaritmi di w o della frequenza f e in ordinata il modulo della G(s) calcolato in dB cioè in decibel.
Nel diagramma della fase metttiamo sulle ascisse la frequenza o w in scala logaritmica e in ordinata i gradi o i radianti dello sfasamento.
Scala semilogaritmica
Esempi di trasformate di Laplace
G(s)= K --> G(s) con K=costante reale o complessa
G(s)= s --> G(s) che ha uno zero nullo per Z=0
G(s)= s+1 --> G(s) che ha uno zero reale per Z=1
G(S)= 1/s --> G(s) che ha un polo nullo per P=0
G(s)= 1/(s+1) --> G(s) che ha un polo reale nel punto P=1
Diagramma di Bode di una G(s) con polo reale p=1
Calcolare il diagramma di Bode di G(s) = 1/(s+1)
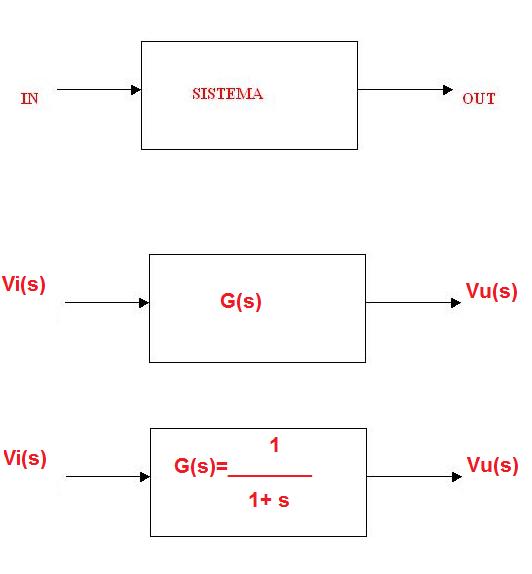
Dato il seguente sistema in catena aperta, che abbia una funzione di trasferimento
G(s)=1/(s+1)
Calcolare il suo diagramma di Bode del modulo e della fase al variare di w.
Calcolo del modulo in decibel della G(s)= 1/(s+1)
La funzione di trasferimento è:
G(s)=1/(s+1)
Calcoliamo il suo modulo in decibel.
|G(s)| dB= 20 log |G(s)|= -20 log (1 +w^2)^ 1/2
Per rappresentare questo modulo in decibel con i diagrammi di Bode basta fare i limiti per alcuni valori di w ben precisi, ad esempio:
lim -20 log (1 +w^2)^ 1/2 = 0
w->0
lim -20 log (1 +w^2)^ 1/2 =00
w->00
lim -20 log (1 +w^2)^ 1/2 = -3 dB
w->1
lim -20 log (1 +w^2)^ 1/2 = -20 dB
w->10
lim -20 log (1 +w^2)^ 1/2 = 0, 04
w->0,1
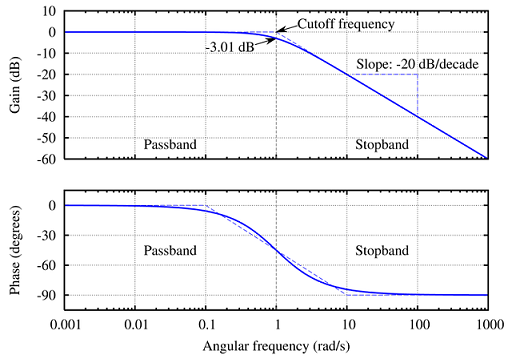
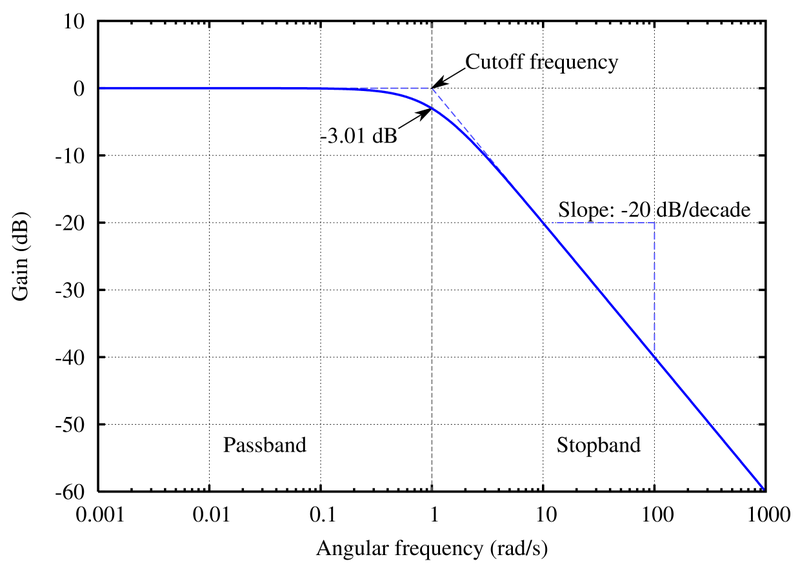
Riportando il grafico di |G(s)| dB su scala semilogaritmica avremo il grafico di un filtro passa basso con il polo p=1
Calcolo della fase di G(s)=1/(s+1)
Per calcolare la fase di
G(s)=1/(s+1)
ricordiamo che la fase di un numero complesso si ricava con la formula
fase(G(jw))= arctg( Im/Re)
Trasformaiamo quindi la G(s) in G(jw).
Ricordando che s=jw avremo:
G(jw)= 1/(1+jw)
e quindi
fase(Gjw)= - w/1
Il segno meno viene vuori dal fatto che la funzione G(s) ha la variabile s al denominatore.
Calcoliamo quindi i limiti per ricavare il diagramma asistotico;
sono necessari solo tre punti cioè il limite per
w=polo=wp,
w=0
w=00;
possiamo anche calcolare w = 0,1Wp e w =10 wp cioè la decade precedente al polo e la decade successiva al polo.
lim fase G(jw)= lim -arctg w= 0°
w-->0 w-->0
lim fase G(iw) = lim - arctg w= -90°
w-->00 w-->00
lim fase G(jw)= lim - arctg w= -45°
w-->1 w-->1
si possono anche calcolare i limiti della fase di G(jw) nella decade precedente al polo cioè per w=0,1 e per la decade successiva al polo per w=10.
Riportando questi valori nel grafico semilogaritmico in cui in ascisse mettiamo w e in ordinate la sua gase in gradi avremo il diagramma di Bode della fase.
G(s) del filtro passa basso RC
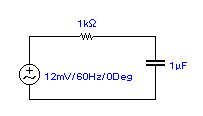
Esercizio:
Calcolare la G(s) di un filtro RC e disegnare il suo diagramma del modulo e della fase.
Nel filtro RC si ha una
G(s)= Vu(s)/Vi(s)= (1/Cs)/ ( R+ 1/Cs)= 1/(1+ RC*s) -->
G(S)= 1/(1+RCs)
essendo il polo p della G(s)
p= 1/RC=w
w=2*3.14*f =1 /RC -->
la frequenza di taglio del filtro passa basso è
f =1/( 2*3.14 * RC ) =1/RC
Di solito la costante RC viene chiamata tau (lettere greca) ed ha la dimensione del tempo misurato in seconti cioè
tau= RC=[s]
se il filtro è di tipo RC e
1/RC=[Hz]
Facendo tutti i i limiti della funzione |G(s)|dB , come nell'esercizio precedente), si dimostra che , nel polo p= 1/RC e quindi anche nella frequenza di taglio si ha una attenuazione di - 3dB pari ad una diminuzione del 30% dell'amplificazione ( vedi grafico del diagramma di Bode del modulo in dB).
Il filtro RC e' quindi di tipo passa basso in quanto per pulsazioni inferiori alla pulsazione di taglio si ha |G(s)|dB uguale a zero, dopo la pulsazione di taglio ( o frequenza di taglio), si ha una attenuazione di -20dB/dec, mentre nel polo ( o nella frequenza di taglio) si ha una attenuazione di -3dB ( o del 30%).