La matematica ha una lunga tradizione presso tutti i popoli della storia antica e moderna; è stata la prima disciplina a dotarsi di metodi di elevato rigore e portata. Ha progressivamente ampliato gli argomenti della sua indagine e progressivamente ha esteso i settori ai quali può fornire aiuti computazionali e di modellizzazione.
Equazioni matematiche, grafici e segnali di prova
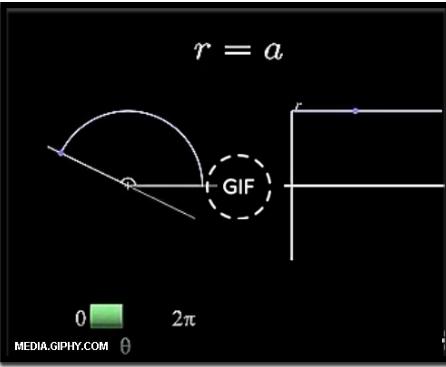
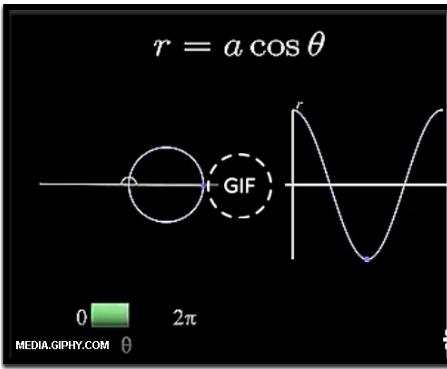
Le equazioni matematiche ci esprimono in modo semplice le equazioni di diversi segnali di prova che possono essere utilizzati in elettronica. In queste immagini vediamo alcuni esempi.
Esercizio
Segnali di prova: Gradino di tensione costante
Supponiamo di avere un segnale costante come quello generato da una pila o da una batteria considerati ideali.
Questi generano una tensione costante e quindi in elettronica possono chiamarsi anche gradino o scalino.
Possono essere considerati gradini, anche la tensione generata da un interruttore, nel senso che se l'interruttore è spento (tasto aperto) la sua tensione in uscita è Vu=0Volt, mentre se l'interruttore è cacceso (tasto chiuso) la sua tensione di uscita ' Vu= costante.
Equazione di un segnale costante ( o segnale costante):
sca(t)=costante per t>=0 e
sca(t)=0 per t<0
Questo segnale non è altro che il gradino di tensione ( assimilabile anche ad una batteria o ad un segnale costante ) che viene acceso (tasto ON) nell'istane t=0 e rimane costante per t>0.
Il segnale sinusoidale
Segnale sinusoidale
y(t)= Vmax * sin w t
Questo segnale è il segnale alternato di tipo sinusoidale con :
Vmax= ampiezza del segnale
w= 2* pigreco* f = 2 * pigreco/ T -> w è la pulsazione
Il segnale di tensione a rampa
Una rampa di tensione è un segnale crescente di equazione:
V(t)= k* t
dove k è il coefficiente angolare della rampa.
Se K=1 la rampa è detta rampa unitaria e la tensione risulterà proporzionale al tempo t:
V(t)= t
La rampa può essere con coefficiente angolare k positivo, e in questo caso la rampa è crescente, oppure con coefficiente angolare k negativo e in questo caso la rampa è decrescente.
Se vi è un susseguirsi di rampe crescenti e decrescenti periodiche il segnale è triangolare.
L'equazione dell'iperbole
y=1/x
esprime la proprietà che la variabile x è inversamente proporzionale a y.
L'equazione del cerchio
x^2 +y^2=9
esprime l'equazione di un cerchio con raggio r=3 --> r^2=9
L'equazione di una rampa ( o retta passante per l'origine)
y=2x
esprime una retta passante dall'origine con coefficiente angolare m=2:
se consideriamo il modulo di
y=| -2x| otteniamo il grafico di una rampa speculare con l'asse y.
L'equazione sinusoidale
x=3 siny
esprime l'espressione della funzione seno moltiplicata per il numero 3.;
se consideriamo il modulo
x=-3 |siny|
otteniamo la funzione seno simmetrica rispetto all'asse x.
Grafici delle funzioni
Introduzione alle equazioni di secondo grado
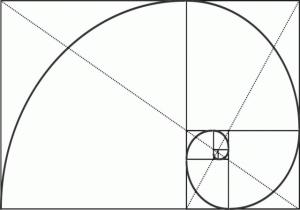
Matematica e bellezza: il numero Phi
Dal 1500 era noto che le figure geometriche le cui proporzioni rispettano la proporzione divina sono più gradevoli ai sensi umani. Molti artisti, quali pittori, scultori, architetti e musicisti, hanno basato la costruzione delle loro opere sul numero aureo, spesso anche inconsciamente. Per esempio nella Piramide di Cheope la proporzione divina si nasconde nel rapporto tra il semilato e l'altezza della piramide, infatti, in tal caso, si ha
{186,64m}/{115m}=1,6229 .
Altri esempi del suo utilizzo nell'arte sono offerti da Leonardo da Vinci che ha realizzato diverse sue opere, tra cui la Gioconda, usando come base la costruzione del rettangolo aureo.
La proporzione divina non è solo appannaggio degli artisti e delle opere d'arte, ma è anche largamente presente in natura. È presente nelle spirali dei semi di girasole, nelle spirali delle pigne, nella disposizione delle foglie sui rami e così via. La cosa più sorprendente è
che in genere regola il rapporto tra il tutto e una sua parte, per cui il rapporto tra il proprio braccio e l'avambraccio o il rapporto tra la propria altezza e la lunghezza dal bacino ai piedi saranno delle buone approssimazioni del numero phi.
Giochino matematico
Voti scolastici
Adesso diamoci un voto per le nostre conoscenze.
Tu che voto ti daresti? Risposta(......)
Il tuo insegnante che voto ti da? Risposta (.....)
-Se i due voti sono uguali ti sei giudicato bene
-Se i due voti sono diversi:
Rifletti e pensa sempre positivo: puoi sempre migliorare.
Media aritmetica:
media dei voti = ( voto 1 + voto2 + voto 3+.....+ voto n) / n
In elettronica se il segnale è sinusoidaleil suo valore picco-picco è:
Valore picco picco di un segnale è:
Vpp= 2* Vmax
Invece il suo valore medio in metà periodo è:
Vmedio= Vmax/ pi greco
Il suo valore medio in un perido è:
Vmedio=0
Contare in basi diverse
Il MONDO BINARIO
Nel mondo binario si conta in base 2.
Il binario ha solo le cifre 0 e 1.
IL MONDO DI TRIX.
Nel mondo di Trix si conta in base tre.
Trix conosce solo tre cifre: 'o, 1,2.
Il MONDO di PENTIX L'EXTRATERRESTRE SPECIALE.
Nel mondo di Pentix si conta in base cinque. ,
Pentix conosce solo cinque cifre: 0, 1,2,3,4.
Con queste cifre riesce a scrivere tutti inumeri
che vuole.
IL MONDO OTTALE
OTTILAND IL PIANETA DOVE SI CONTA IN BASE OTTO.
Nel mondo di Ottix si conta in base otto.
Ottix conosce solo le cifre: O, 1, 2, 3, 4,5,6, 7.
Con queste cifre riesce a scrivere tutti i numeriche vuole.
Formule inverse
In elettronica la matematica è di fondamentale importanza.
Una delle primissime leggi che si studiano è la legge di OHM e non conoscendo bene la matematica molti studenti hanno dei problemi con le formule inverse:
V= R* I
R= V/I
I= V/R
e così via con tuttele altre formule di elettronica, di cui vogliamo calcolarci le formule inverse.
Naturalmente a complicare la vita ai nostri studenti sono anche tutte quella formule con i numeri complessi, i vettori, il piano di Gauss, i diagrammi di Bode, i digrammi di Nyquist, le trasformate di Laplace e così via.
Indovinelli matematici
Se...
2 + 3 = 10
7 + 2 = 63
6 + 5 = 66
8 + 4 = 96
... allora
9 + 7 = ?
Indovinello matematico 2
Sapresti dire quale logica lega i seguenti numeri?
5 – 10 – 2 – 9 – 8 – 4 – 6 – 7 – 3 – 1
Indovinello matematico 3
Una lumaca si trova alla base di un muro alto 20 metri.
Ogni giorno sale di 5 metri ma, durante la notte, scivola in giù di 4.
In quanti giorni la lumaca raggiungerà la cima del muro?