La resistenza elettrica è una grandezza fisica scalare che misura la tendenza di un corpo ad opporsi al passaggio di una corrente elettrica, quando sottoposto ad una tensione elettrica.

Questa opposizione dipende dal materiale con cui è realizzato, dalle sue dimensioni e dalla sua temperatura.

Uno degli effetti del passaggio di corrente in un conduttore è il suo riscaldamento (effetto Joule).

La resistenza R è l'inverso della conduttanza elettrica G, definita come:

R= 1/G

ed anche

 R= 1/G= ρ*L/S= L/(σ * S)

dove:

σ è la conducibilità elettrica misurata in S/m, mentre il suo inverso ρ è la resistività elettrica;

L è la distanza (misurata in m) dei punti tra i quali è misurata la resistenza;

S è l'area della sezione del campione perpendicolare alla direzione della corrente (misurata in m^2).

Nel sistema internazionale l'unità di misura della resistenza elettrica è l'Ohm(Ω).

Esiste la seguente proprieta':

R= ΔV/I

dove:

ΔV la tensione a cui è sottoposto il corpo
I è l'intensità di corrente che attraversa il corpo

Essa esprime la legge di Ohm in forma macroscopica solo per componenti a geometria costante o più precisamente per L e S costanti.

La legge di OHM è di fondamentale importanza nei circuiti elettronici.

Essa dice che esiste una proporzionalità diretta tra la tensione applicata ad un cicuito e la corrente in esso circolante, chiamata resistenza, cioè

R= V/ I

dove V è la tensione applicata nel circuito ed I è la corrente in esso circolante.

La resistenza si misura in Ohm in onore al nome del suo scopritore.

La tensione si misura in Volt e la corrente in Ampère.

Dalla formula precedente si ricavano anche le formule inverse:

 V= R * I

I= V/R

Per calcolare le resistenze in serie si utilizza la formula:

Rs= R1+ R2+R3+R4+R5

Il calcolo della corrente si può fare in ogni ramo utilizzando un amperometro oppure teoricamente con la formula:

I= V /Rs

da cui

I = V / (R1+R2+R3+R4+R5)

Per calcolare la resistenza in parallelo si utilizza la formula:

Rp=R1*R2/(R1+R2)

Il calcolo della corrente si può fare in ogni ramo utilizzando un amperometro oppure teoricamente con la formula:

I= V/Rp se il circuito ha resistenze in parallelo.

La potenza è il lavoro fatto nell'unità di tempo

P= L/ t

La sua unità di misura+

P=[Joule/s]=[Watt]

La potenza elettrica è data da

P=V*I

Per verificare quest'ultima formula basta ricordarsi che il lavoro L si misura in elettronica in eV cioè in elettronVolt, dove l'elettrone non è altro che la carica elettrica Q e Volt è l'unità di misura della tensione.

Sostituendo al posto del lavoro L la formula Q*V si ha:

P= L/ t = Q*V/ t = V*I        (1)

La potenza elettrica può anche assumere alre forme ricordando la legge di Ohm

V=R*I

Infatti, se nella  (1) sostituiamo al posto della V il valore V=R*I otteniamo

P= R * I^2

Se invece sostituiamo nella  (1) al posto della I il valore I= V/R otteniamo

P= V^2 / R

La potenza totale di un circuito si suddivide in tutti gli utilizzatori. Per sempio se abbiamo 3 resistenze la potenza totale del generatore è uguale alla somma delle potenze sulle singole resistenze. 

In formula diventa:

P(totale) = P1 +P2 + P3

dove P(totale) è la potenza del generatore data da 

P(totale) = V(totale)* I (totale)

mentre 

P1= R1 * I1

P2= R2 * I2

P3 = R3 * I3

Dato che il circuito è in serie la corrente I(totale) uscente dal generatore è uguale alla corrente I circolante nelle singole resistenze; da ciò segue che:

P(totale) =  R1* I1 + R2* I2 + R3* I3 = (R1+ R2 +R3 )* I = R(totale) *I

I teoremi di Kirchhoff sono due, teorema applicato alla maglia e teorema applicato ad un nodo.

Teorema di Kirchhoff applicato alla maglia:

La somma algebrica di tutte le cadute di tensioni in una maglia ( cioè prese con il proprio segno) è uguale a zero.

oppure:

Se in una maglia ci sono n resistenze  la tensione di alimentazione si suddivide in tutte le resistenze:

VAL = V1 +V2 +V3 +... +Vn = I1*R1 + I2*R2 +I3*R3 +.....+ In* Rn)

 madato che in una maglia le resistenze sono in serie, la corrente circolante è sempre la stessa, segue che:

VA L = I*(R1+R2+R3*...Rn) = I* R(serie)

Teorema applicato ad un nodo

In un nodo la somma delle correnti entranti è uguale alla somma delle correnti uscenti dal nodo.

Oppure:

In un nodo la somma delle correnti entranti ed uscenti presi ognuna con il proprio verso di percorrenza è uguale a zero.

Se nel nodo A abbiamo tre correnti entranti e tre correnti uscenti si ha:

I1+I2+I3 = I4+I5+I6

oppure

I1+I2+I3 - I4 - I5 - I6 =0

Il teorema di Millman si applica ad una rete con tanti Rami tutti derivati da dua Nodi a e b. 

Esso afferna che «la tensione ai capi del bipolo della rete è data dal rapporto tra la somma algebrica delle correnti di corto circuito dei singoli rami e la somma delle conduttanze di ogni ramo». In formula si ha

Vab= ( I1cc/R1 + I2cc/R2 + I3cc/R3 +.... +Iccn/Rn) / ( 1/R1 + 1/R2 +1/ R3 +...+ 1/Rn)

ESEMPIO:

Nel circuito binodale con tre rami in parallelo  si ha che:

Vab( 1/R1 +1/R2 + 1/R3)=  (Icc1+ Icc2 +Icc3) =  Icc(totale)

--> Vab= Icc(totale)*R(totale) =(Icc1+ Icc2 +Icc3)* ( 1/(1/R1 + 1/R2 +1/R3)) =

Vab=Icc1+ Icc2 +Icc3) / ( 1/R1 +1/R2 + 1/R3)

Vab= (V1/R1 +V/R2 +V3/R3) / ( 1/R1 +1/R2 + 1/R3)

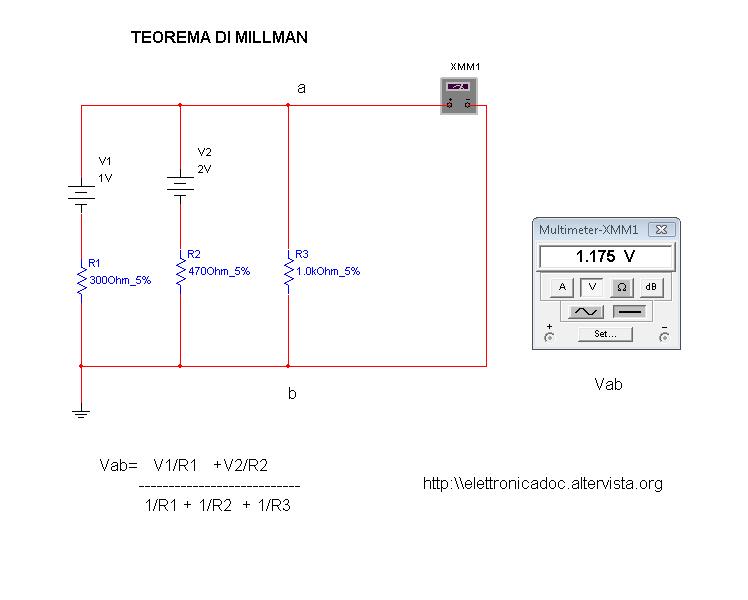
CASO PARTICOLARE:

Nel caso in cui in un ramo non c'è alcuna batteria, la sua corrente di cortocircuito in quel ramo è uguale a zero.

Guardiamo il precedente circuito. In un ramo non c'è la batteria e quindi la sua corrente di corto circuito è uguale a zero. Applicando Milmann si ha:

Vab=  (V1/R1 + V2/R2) / (1/R1+ 1/R2 +1/R3)

Sostituiamo i valori numerici:

Vab= (1/300 + 2/470)/( 1/300+ 1/470 + 1/1000) = (0,003+ 0,004) / (0,003 + 0,002 + 0,001) = 0,00758/0,0064 -->

Vab= 1,175 V

Dato il seguente circuito con resistenze, calcolare tutte le tensioni e tutte le correnti circolanti, utilizzando i valori delle figure e risolverli con qualunque metodo di tua conoscenza.

Risolvere il seguente circuito utilizzando il teorema di THEVENIN;

calcolare tutte le tensioni e le correnti .

Risolvere il seguente circuito calcolando la resistenza totale, la corrente uscente dal generatore e le correnti circolanti nelle due maglie.

Verificare il teorema di Kirchooff  seguente:

"La corrente entrando in un nodo e' uguale alla somma delle correnti uscenti dal nodo".

Calcolare tutte le tensioni e tutte le correnti del seguente circuito e la resistenza totale.

Calcolare la resistenza equivalente tra i punti A e B con generatore di tensione aperto.