Schemi a blocchi
Gli schemi a blocchi costituiscono un formalismo per rappresentare graficamente le interazioni tra sistemi dinamici.
Vediamone gli elementi costitutivi:
Il blocco
Il blocco non è altro che un simbolo indicante la presenza di un sistema dinamico, avente la funzione di trasferimento riportata nel simbolo del blocco, e l’ingresso e l’uscita riportati rispettivamente sulla freccia entrante e sulla freccia uscente dal blocco:
La risposta nel dominio di s è
Y(s)=G(s)*X(s)
dove X(s) viene anche chiamata sollecitazione di ingresso o segnale in ingreso, e G8s) è la funzione di trasferimento
G(s)=Y(s)/X(s)
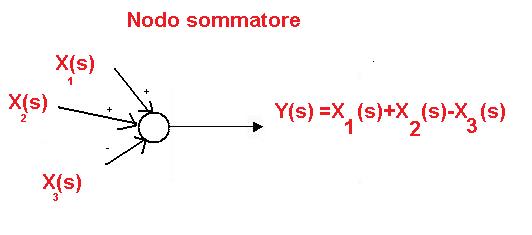
Il nodo sommatore
L’uscita del nodo è data dalla somma algebrica dei segnali che entrano nel nodo, ciascuno preso con il proprio segno (se non è indicato il segno, si assume per convenzione il segno positivo).
Punto di diramazione
Tutti i segnali uscenti da un punto di diramazione sono uguali al segnale entrante nel punto.
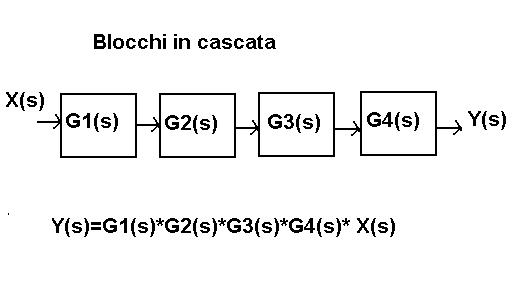
Sistemi in cascata
Due sistemi si dicono in cascata (o in serie) se l’uscita di uno è l’ingresso dell’altro. Graficamente si ha la seguente situazione:
La funzione di trasferimento dall’ingresso del primo sistema all’uscita del secondo si ottiene come segue:
Y(s)=G1(s)*G2(s)*G3(s)*G4(s)*X(s)
La funzione di trasferimento del sistema costituito dalla cascata di più sottosistemi è data dal prodotto dei singoli sottosistemi per il segnale di ingreso X(s).
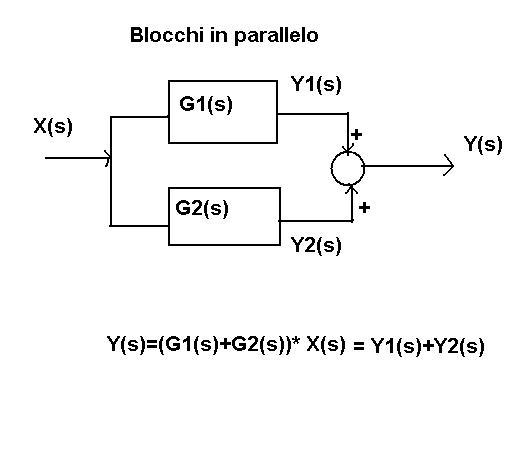
Blocchi in parallelo
Due sistemi si dicono in parallelo se hanno lo stesso ingresso, mentre le loro uscite si sommano (algebricamente) per determinare l’uscita del sistema risultante. Graficamente si ha la seguente situazione:
La funzione di trasferimento dall’ingresso comune ai due sistemi all’uscita si ottiene come segue:
Dato che
Y1(s)=G1(s)*X(s)
Y2(s)=G2(s)*X(s)
allora
Y(s)=Y1(s)+Y2(s)=G1(s)*X(s)+G2(s)*X(s)=(G1(s)+G2(s))*X(s) -->
Y(s)=(G1(s)+(G2(s))*X(s)
Cioè il segnale di uscita del sistema è dato dalla somma delle funzioni di trasferimento dei singoli blocchi moltiplicati per il segnale di ingresso.
Oppure:
La funzione di trasferimento del sistema costituito dal parallelo di due sottosistemi è quindi data dalla somma algebrica delle due funzioni di trasferimento parziali, ciascuna presa con il segno con cui la sua uscita entra nel nodo sommatore cioè:
Y(s)/X(s)= G1(s)+G2(s)
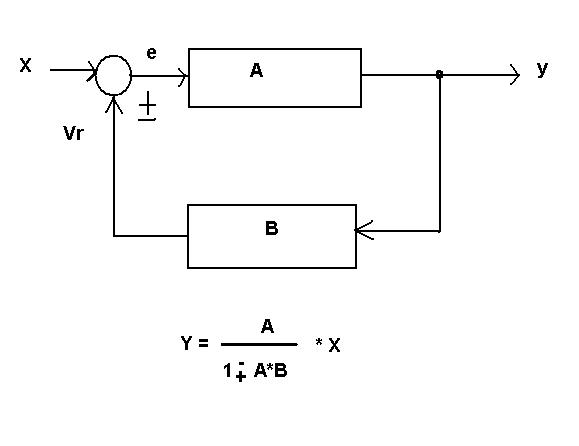
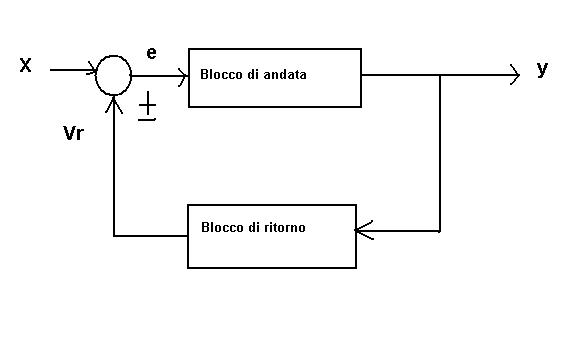
Sistemi in retroazione
Due sistemi si dicono connessi in retroazione quando l’uscita del primo è l’ingresso del secondo, mentre l’uscita del secondo si somma o si sottrae ad un ingresso esterno per determinare l’ingresso del primo sistema. Si hanno quindi due possibili schemi di connessione:
Uno con retroazione positiva e l'altro con retroazione negativa.
Entrami i sistemi li posiamo considerare con il seguente blocco:
Dove y è la risposta del sistema
X il segnale di ingresso o sollecitazione di ingresso
A e B sono due cstanti o due funzioni, una nel blocco di andata e una nel blocco di ritorno.
Facendo un pò i conti si trova che
y=(A/(1-/+A*B))*x
Di solito il segnale retroazionato viene anche chiamato Vr, mentre il segnale che rientra nel sistema viene chiamato e o segnale di errore.
Notiamo che se la retroazione Vr è positiva al denominatore della (1) dobbiamo mettere il segno - (meno) mentre se la retroazione Vr è negativa al denominatore della (1) dobbiamo mettere il segno + (più).
Questo segno al denominatore è molto importante perchè individua se il sistema ha una retroazione positiva (sgno meno al denominatore) o una retroazione negativa (segno più al denominatore).
Segnale di Errore
Il segnale di errore e è dato dalla somma o dalla differenza del segnale di ingresso e il segnale di retroazione:
e= x + Vr
Inoltre se stiamo considerando il sistema nel dominio del tempo si ha:
e(t)= x(t) + Vr(t)
mentre se siamo nel dominio di s
E(s)= X(s) + Vr(s)