In elettrotecnica con il termine sistema trifase si intende un sistema combinato di più circuiti a corrente alternata (di produzione, distribuzione e utilizzazione dell'energia elettrica) aventi la stessa frequenza (isofrequenziali) e tre tensioni alternate uguali, ma sfasate tra loro di 120°.

Rispetto ad un sistema a corrente alternata monofase il costo del materiale e dei cavi elettrici viene dimezzato con una potenza elettrica pari.

Quando si lavora in sistemi di produzione, distribuzione e utilizzazione dell'energia elettrica si usa chiamare generatore monofase un generatore di tensione sinusoidale.

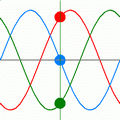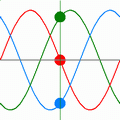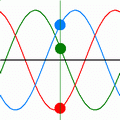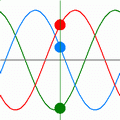
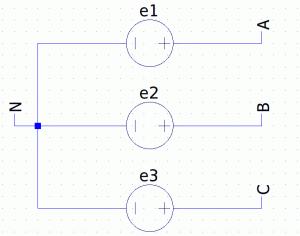
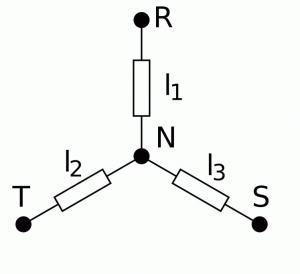
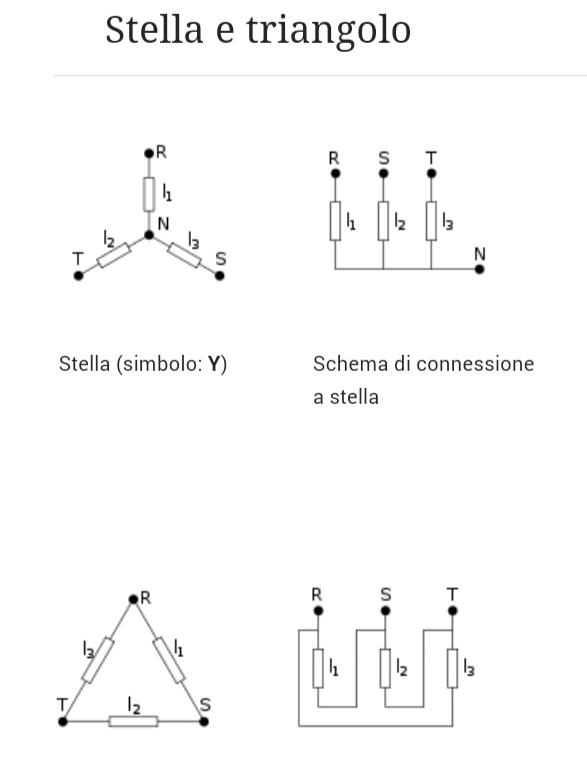
Un generatore trifase può essere ottenuto collegando tre generatori monofase sinusoidali, isofrequenziali in modo da costituire un tripolo (si veda la figura). La connessione è detta a:

--> Stella, se i tre generatori condividono un terminale,
--> Triangolo, in caso contrario

Alle tensioni di  [e_1(t)] ,  [e_2(t)]  e  [e_3(t)]  si dà il nome di tensioni stellate.

Corrispondono ai potenziali dei nodi A,B,C.

È possibile definire le tensioni concatenate nel modo seguente:

[u_{AB}(t)=e_1(t) - e_2(t)]

[u_{BC}(t)=e_2(t) - e_3(t)]

[u_{CA}(t)=e_3(t) - e_1(t)]

Nel caso di sistema trifase simmetrico ed equilibrato i tre generatori singoli monofase che costituiscono il generatore trifase, sono isofrequenziali (cioè con la stessa frequenza) e le fasi differiscono di  2/3 pi greco  (120°).

La potenza attiva assorbita da un carico trifase, che è quella considerata al fine della fatturazione, può essere ottenuta sommando le potenze misurate sulle singole fasi. Per ogni fase, considerata la tensione V tra fase e neutro, l'intensità della corrente I e l'angolo di sfasamento (tra tensione e corrente) φ, vale

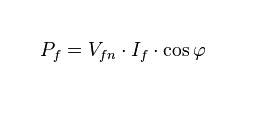
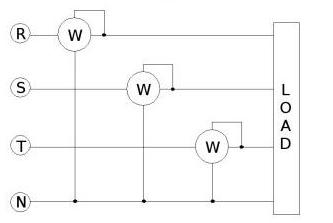
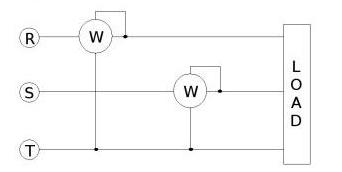
il circuito di misura è il seguente

Se non è presente il neutro si può immaginare di realizzare un circuito simile al precedente, in cui come riferimento per le tensioni di due fasi è utilizzata la terza linea. Si può realizzare il seguente circuito di misura:

Questa configurazione a tre fili è comunemente utilizzata nella pratica ed è nota come inserzione Aron.

La potenza totale è data dalla somma algebrica del valore indicato dai wattmetri.

Se il carico è equilibrato e puramente resistivo l'indicazione dei due strumenti è identica, se invece il carico ha una componente induttiva il valore indicato dal primo wattmetro in ordine di rotazione delle fasi (la sequenza temporale con cui iniziano i cicli dell'onda) indica un valore maggiore del secondo.

La situazione è opposta nel caso di un carico a componente capacitiva.

Se lo sfasamento supera il limite di 60° lo strumento di valore minore inizierà a fornire un valore negativo, fino a che in teoria i due strumenti daranno indicazioni uguali in modulo ma opposte per carichi puramente reattivi (potenza attiva pari a zero).

Il metodo Aron può anche essere utilizzato per leggere il valore della potenza reattiva dei carichi equilibrati.

La potenza reattiva Q si ottiene moltiplicando per radice di 3 la differenza tra le letture dei due wattmetri.

La grande importanza del sistema trifase è dovuta a tre fondamentali vantaggi:

- momento di rotazione;
- ottimizzazione dei conduttori;
- minori perdite di trasporto.

L'ultilizzo del sistema trifase in bassa tensione (230 V) si ha con utilizzatori di media e alta potenza, mentre per la bassa potenza si usa il sistema monofase.

In media e alta tensione (II e III categoria) si usa esclusivamente il sistema trifase.
In un sistema monofase abbiamo a disposizione due cavi (fase e neutro), mentre in un sistema trifase abbiamo generalmente a disposizione quattro cavi (tre fasi e un neutro comune).

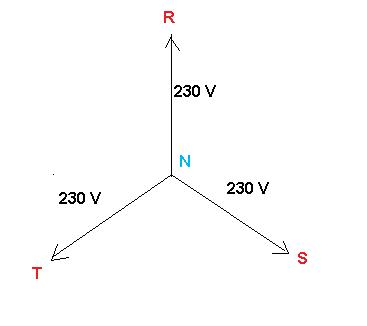
Graficamente il potenziale del neutro è rappresentato dal punto N di applicazione dei vettori e ogni fase ha una differenza di potenziale rispetto al neutro di 230 volt (rappresentata dalla lunghezza di ogni vettore).

Tra fase e neutro abbiamo una differenza di potenziale di 230 volt

Tra due fasi abbiamo una differenza di potenziale di 400 volt

I cavi che vengono utilizzati per l’impianto elettrico, invece, sono 3, ognuno di un colore diverso: uno nero per la fase corrente (vengono utilizzati anche di colore rosso, grigio o marrone), uno blu per il neutro e uno giallo-verde per la messa a terra.

Le prese vengono installate a 30cm da terra mentre gli interruttori a 1 metro circa da terra. In stanze come il bagno e la cucina possono essere installate prese anche a un 1m/1,20m per essere più funzionali nell’uso.

In teoria dei sistemi, probabilità e Ingegneria dell'affidabilità, definendo come "qualità" di un assieme o di un sistema più o meno complesso la sua rispondenza ai criteri di specifica tecnica di funzionamento, si definisce affidabilità la capacità di rispettare le specifiche tecniche di funzionamento nel tempo.

L'affidabilità di un insieme (un apparato elettronico, una macchina, ecc.), di un sistema comunque complesso o di un semplice componente (ad esempio una resistenza elettrica) è la misura della probabilità che l'assieme (o il componente) considerato non si guasti (ovvero non presenti deviazioni dal comportamento descritto nella specifica) in un determinato lasso di tempo.

Per semplicità, in seguito (se non diversamente indicato) si parlerà di "componente" riferendosi sia ad un assieme o sistema complesso sia ad un componente elementare.

L'importanza del concetto di affidabilità è tale che, in ambito applicativo, esiste una disciplina ad essa dedicata: l'ingegneria dell'affidabilità.

In tale contesto, per superare le difficoltà in termini di affidabilità di un sistema, è stato introdotto il concetto di ridondanza nell'ambito del dimensionamento dei sistemi fisici realizzati.

In senso esteso, il termine "affidabilità" può riferirsi anche alla validità o meno delle teorie scientifiche e delle loro intrinseche previsioni.

Un guasto (in inglese fault) è un evento per cui un sistema viola definitivamente le specifiche di funzionamento, interrompendo la disponibilità dei servizi che fornisce.

L'affidabilità è la probabilità che tale sistema non si guasti si dice funzione di sopravvivenza ed è definita essere 

R(t)=1-F(t)

Da un punto di vista matematico, interpretando il tempo di guasto come una variabile casuale continua, F è la sua funzione di ripartizione e R il suo complemento a uno.

Se si considera un componente elementare, ad esempio una resistenza elettrica in condizioni di lavoro ben determinate, l'affidabilità è evidentemente dovuta unicamente a tale componente. È diverso il caso in cui un assieme sia costituito da più componenti: il valore di affidabilità dipenderà dalle affidabilità di ciascun singolo componente.

Per la proprietà dell'assenza di memoria, l'affidabilità di un componente elettronico è calcolata con la legge esponenziale negativa, che approssima anche componenti meccanici che nel ciclo di vita (progettuale) del prodotto non hanno ancora iniziato la fase di degrado: la frequenza dei guasti è ancora dovuta a variabili non correlate all'età del componente.

Ogni volta che la probabilità di guasto è indipendente dall'età (e dal tempo di servizio) dei componenti del sistema, si ipotizza che il tempo del primo guasto e (il tempo di attesa) dei successivi seguano una distribuzione esponenziale negativa, e che il numero di guasti (tasso di guasto λ) segua una distribuzione di Poisson. Le due ipotesi di distribuzione, ore dette, si implicano a vicenda

 R(t)=e^{-lambda t}

Il tempo di attesa tra due guasti successivi può essere stimato dal MTBF noto, mentre il tasso di guasto è ricostruito da un'analisi delle serie storiche di componenti dello stesso tipo ovvero simili dal punto di vista della tecnologia sottostante e della funzionalità dell'utente finale: si calcola la frequenza cumulata dei guasti in funzione delle ore di servizio.

A prescindere dai modelli teorici, in pratica si rileva sul campo l'intervallo medio fra i fallimenti 

MTFB=(Mean Time Between Failure o MTBF o tempo medio fra i guasti)

definito statisticamente come speranza matematica del tempo di funzionamento fra due fallimenti.

Un componente può cessare di funzionare sostanzialmente per due motivi: era già difettoso in origine oppure le sollecitazioni, cumulatesi durante la sua vita operativa, hanno raggiunto il limite massimo per tale componente.

La probabilità di guasto sarà quindi dovuta alla combinazione di due curve:

- la probabilità di avaria per mortalità infantile (preponderante nella primissima fase di vita operativa);
- la probabilità di avaria per sollecitazioni (che si cumula a partire dall'inizio della vita e man mano diviene preponderante).

La curva che ne risulta è detta bathtub (curva a vasca da bagno), che mostra una diminuzione iniziale del numero di fallimenti nel tempo, un periodo di fallimenti costante nel tempo ed infine un aumento del numero di fallimenti nell'unità di tempo.