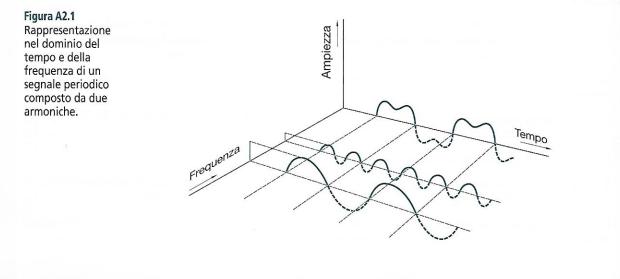
Sviluppo in serie di Fourier

Un segnale determinato può essere rappresentato in funzione della frequenza, riportando in un grafico, denominato spettro, i valori istantanei s(f) che assume al variare della frequenza.

La rappresentazione in funzione della frequenza poggia i suoi fondamentisullo sviluppo in serie di Fourier, il quale, a partire dalla forma d'onda di un segnale periodico, consente di ricavare la composizione spettrale.

Infatti secondo il teorema di Fourier, un segnale periodico s(t) di pulsazione w ( e quindi di frequenza f=w/2PI-greco) può essere scomposto nella somma di un termine costante e di un certo numero di segnali sinusoidali, denominate armoniche, dei quali il primo ha la stessa frequenza d dis(t) e gli altri frequenze multiple di f (2f,3f,4f,...).

Quindi ogni armonica viene rappresentata con un segmento (riga), di lunghezza proporzionale alla sua ampiezza, in corrispondenza del proprio valore di frequenza: l'insieme delle righe costituisce lo spettro del segnale, il quale è pertanto formato da tante da tante righe quante sono le armoniche che lo compongono: un segnale sinusoidale ha pertantouno spettro formato da una sola riga, essendo caratterizzato da una sola frequenza. 

Nella figura precedente è mostrato un esmpio di segnale che comprende soltando le prime due armoniche, rappresentato in un grafico tridimensionale, sia in funzione del tempo, che in funzione della frequenza.

Qualsiasi segnale determinato s(t) periodico di periodo T può essere scomposto nella somma di un termine costante e di un certo numero di segnali sinusoidali dei quali il primo, avente lo stesso periodo di s(t) e quindi la stessa frequenza, è denominata prima armonica o fondamentale e gli altri aventi periodi sottomultipli di s(t) e quindi frequenze multiple, armoniche superiori.

L'enunciato può essere espresso con la seguente relazione:

Il coefficiente a0, che rappresenta il termine costante, costituisce il valore medio di s(t), i coefficienti an e bn le ampiezze delle armoniche di ordine n. Essendo la funzione coseno di tipo pari, e quella seno di tipo dispari, per s(t) pari risultano nulli i coefficienti bn e per s(t) dispari i coefficienti an.

Tramite lo sviluppo in serie di Fourier è pertanto possibile eseguire l'analisi armonica di un segnale s(t) periodico e, viceversa, note le armoniche , riottenere il segnale originario.