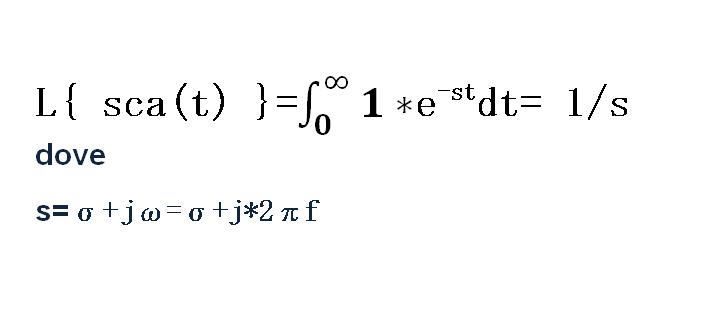Biografia di Pierre-Simon Laplace
Pierre-Simon Laplace, marchese di Laplace (Beaumont-en-Auge, 23 marzo 1749 – Parigi, 5 marzo 1827), è stato un matematico, fisico, astronomo e nobile francese.
Fu uno dei principali scienziati nel periodo napoleonico.
Ha dato fondamentali contributi a vari campi della matematica, dell'astronomia e della teoria della probabilità ed è stato uno degli scienziati più influenti al suo tempo, anche per il suo contributo all'affermazione del determinismo. Laplace, infatti, diede la svolta finale all'astronomia matematica riassumendo ed estendendo il lavoro dei suoi predecessori nella sua opera in cinque volumi Mécanique Céleste (Meccanica celeste) (1799-1825). Questo capolavoro ha trasformato lo studio geometrico della meccanica sviluppato da Newton in quello basato sull'analisi matematica.[1]
Nel 1799 fu nominato ministro degli interni da Napoleone che nel 1806 gli conferì il titolo di conte dell'Impero. Fu nominato marchese nel 1817, dopo la restaurazione dei Borbone.
Le trasformate di Laplace
Sia data una funzione f(t) definita sui numeri reali per t >0.
La sua trasformata di Laplace e' la funzione definita nell'insieme continuo s data da:
L[f(t)] = G(s)
ove
G(s) è l'integrale di f(t) moltiplicato per e^-st in dt, cioè:
NOTA:
Spesso nei libri di sistemi elettronici la funzione F(s) viene anche chiamata G(s). Ricordiamoci che non c'è nessuna differenza nel chiamarla F(s) oppure G(s).
Le trasformate di Laplace sono un argomento molto importante nell'Elettronica e soprattutto nella materia Sistemi Elettronici.
La funzione G(S) =N(S)/D(S) e' la funzione di trasferimento nel mondo complesso di Laplace
Per risolverla bisogna calcolare i Poli del denominatore, cioè le soluzioni dell'equazioni al denominatore dopo averlo posto uguale a zero, mentre gli zeri sono le soluzioni dell'equazione del numeratore dopo che lo abbiamo posto uguale a zero.
La G(S) può quindi essere studiata analizzando i suoi poli e i suoi zeri e poi, con il metodo tabellare o con il metodo delle derivate, possiamo ricondurci, dopo aver calcolato la sua antitrasformata, nella funzione f(t) nel dominio del tempo:
Esempi di trasformate di Laplace
Esempi semplici di G(S) sono :
G(s)= K con K=costante reale o complessa
G(s)= s che ha uno zero nullo per Z=0
G(s)= s+1 che ha uno zero reale per Z=1
G(S)= 1/s che ha un polo nullo per P=0
G(s)= 1/(s+1) che ha un polo reale nel punto P=1
Schemi a blocchi delle funzioni G(s)
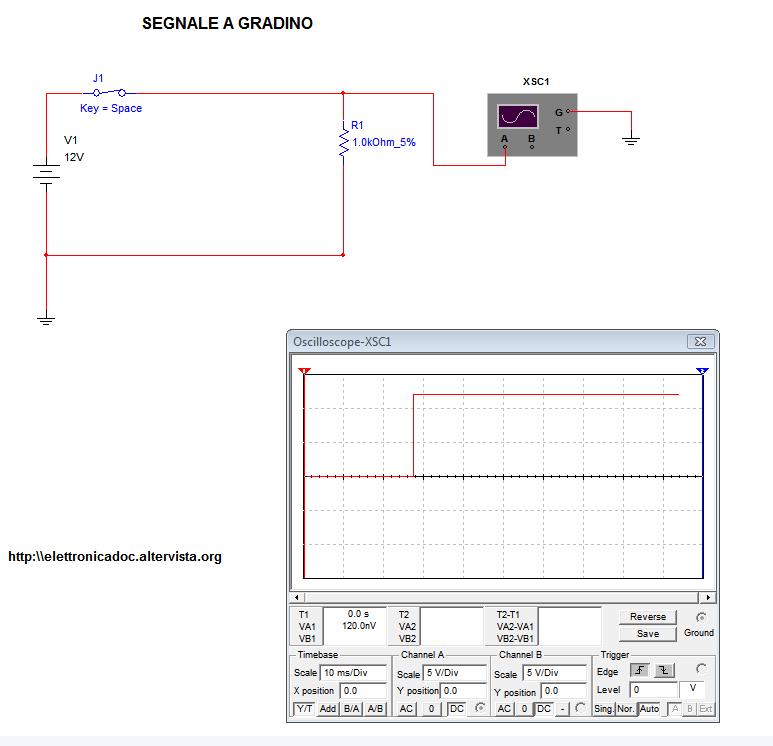
Segnale a gradino e sua trasformata
La funzione scalino o gradino (FUNZIONE DI HEAVISIDE)
f(t)=sca(t) vale 0 per t<0, vale 1 per t>=o
E' una funzione discontinua perchè ha valore zero per argomenti di t negativi e 1 per argomenti di t positivi.
La trasformata di sca(t) è:
La delta di DIRAC
DIMOSTRAZIONE:
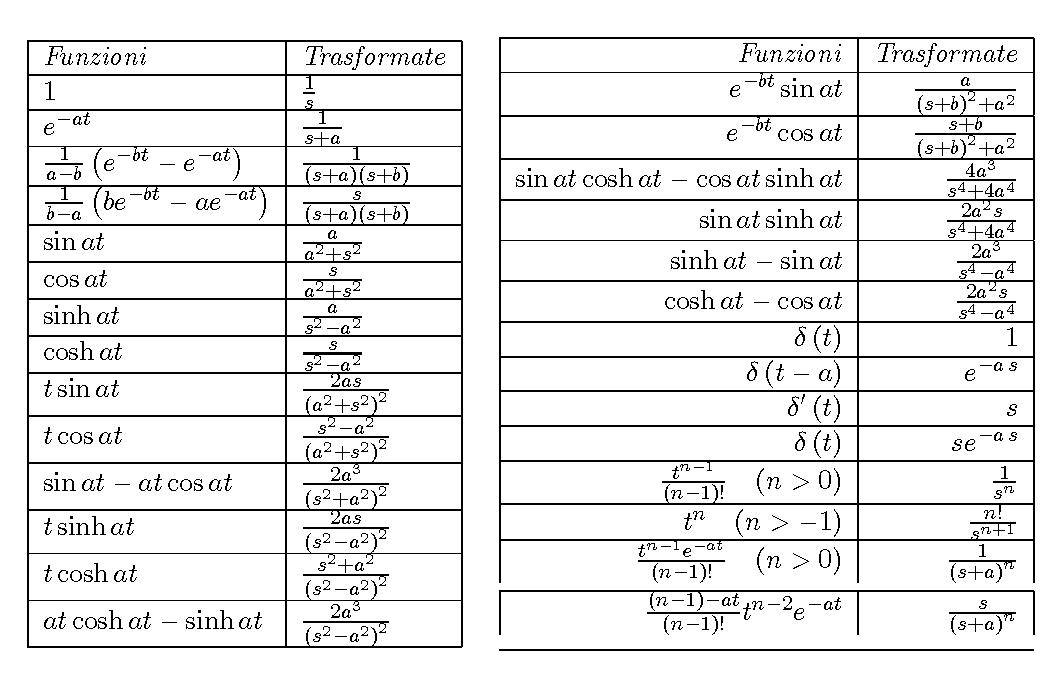
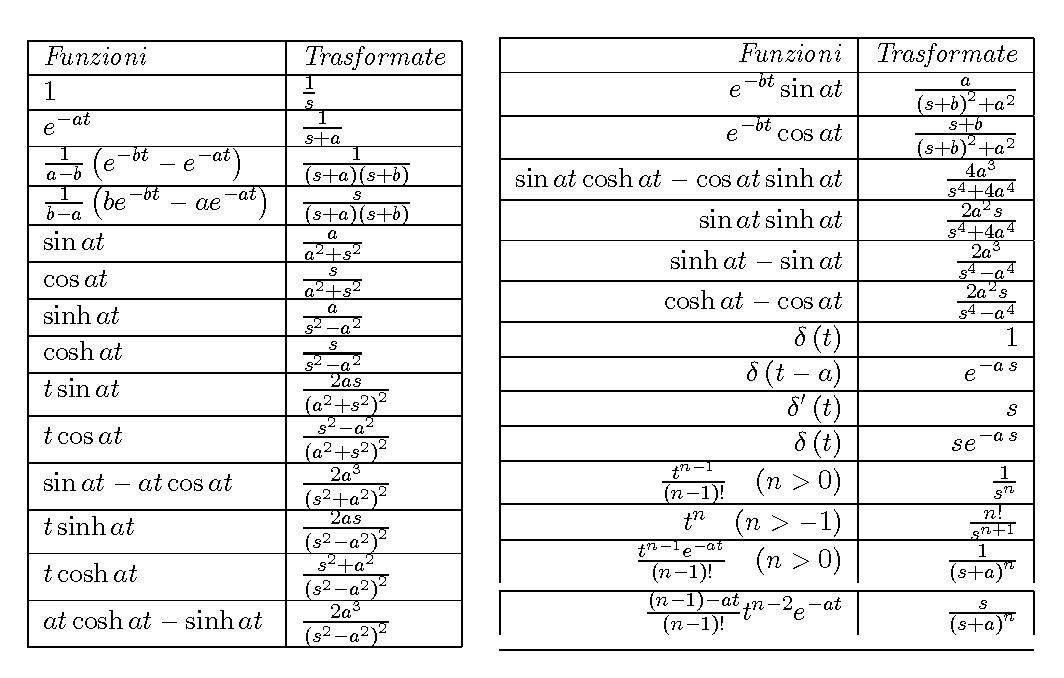
Tabella delle Trasformate di Laplace
Poli e zeri delle trasformate
Definizione di poli e zeri:
In una funzione G(s) si definisce polo il valore di s per cui si annulla il denominatore, si definisce zero il valore di s che annulla il numeratore.
Data la funzione
G(s)= N(s)/D(s)
dove
N(s)= funzione al numeratore nella variabile s
D(s)= funzione al denominatore nella variabile s.
Esempio:
Calcolare i poli e gli zeri della seguente funzione:
G(s)= (s+1)/(s+2)*(s+3)
ha uno zero per s = -1 --> z1=- 1
ha due poli per s= -2 e s=- 3 --> p1=- 2 e p2=- 3
Tabella delle trasformate e antitrasformate di Laplace
Per calcolare la trasformata o l'antitrasformata di Laplace di una funzione, spesso si usa il metodo tabellare.
Se guardiamo la tabella delle trasformate notiamo che:
- nella colonna a sinistra c'è la funzione f(t)=L^-1[Fs)] che è l'antitrasformata di F(s) nel dominio del tempo, mentre
- nella colonna di destra adiacente c'è la sua trasformata F(s)=L[f(t)] nel dominio di s.
Il metodo tabellare è il più semplice metodo per risolvere le trasformata.
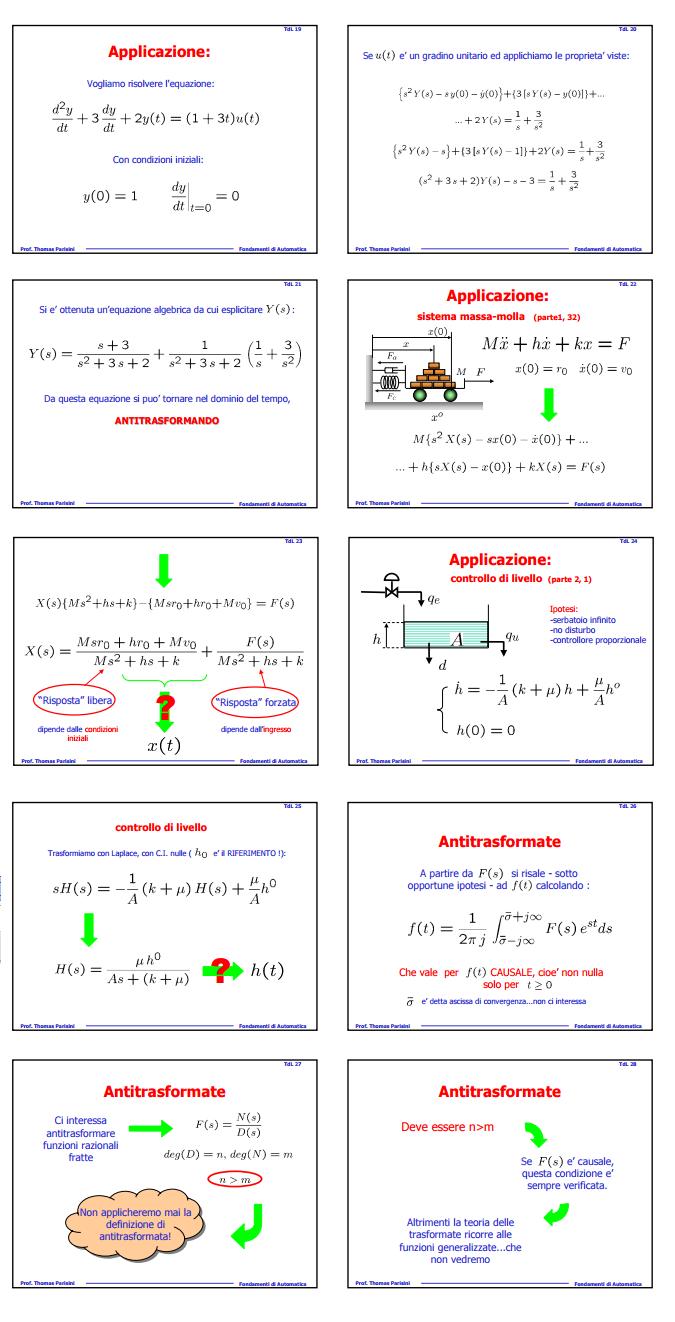
Applicazioni
Esempi di trasformate di Laplace di funzioni G(s) con poli singoli
Esempio 1:
Calcolare l' antitrasformata della seguente funzione
G(s)= 1/( s+5)
questa funzione è del tipo
1/(s+a) che ha come antitrasformata e^(-at) --> essendo a=5 -->
f(t) = e^( - 5t )
Esempio 2:
Calcolare l'antitrasformata di
G(s)= 10/(s+3)
Questa funzione è del tipo
K/(s+a) che ha come antitrasformata K*e^(-at) --> essendo K=10 e a=3 -->
f(t)=10*e^(- 3t )
Esempio 3:
Calcolare l'antitrasformata della funzione
G(s)= 10/( 1 + 2 s)
dividendo numeratore e denominatore per 2 si ha:
G(s)= (10/2)/( 1/2 +s)= 5 / (1/2 +s)
è del tipo K*e^(-at) dove K=5 e a=1/2 -->
f(t)= 5* e ^(- t/2)
Diagrammi di Bode
I diagrammi di Bode sono delle rappresentazioni grafiche della funzione G(s). Esistono due tipi di rappresentazione grafiche:
1)Diagramma del modulo in decibel al variare di w o della frequenza
2)Diagramma della fase al variare di w o della frequenza.
Il diagramma del modulo di G(s) in decibel cioè |G(s)| dB e il diagramma della fase di G(s) al variare di w o della frequenza sono dei grafici in scala semilogaritmica.
Nel diagramma del modulo sulle ascisse mettiamo i logaritmi di w o della frequenza f e in ordinata il modulo della G(s) calcolato in dB cioè in decibel.
Nel diagramma della fase metttiamo sulle ascisse la frequenza o w in scala logaritmica e in ordinata i gradi o i radianti dello sfasamento.
Scala semilogaritmica
ESEMPIO:
Calcolare il diagramma di Bode di G(s) = 1/(s+1)
Dato il seguente sistema in catena aperta, che abbia una funzione di trasferimento
G(s)=1/(s+1)
Calcolare il suo diagramma di Bode del modulo e della fase al variare di w.
Calcolo del modulo in decibel della G(s)= 1/(s+1)
La funzione di trasferimento è:
G(s)=1/(s+1)
Calcoliamo il suo modulo in decibel.
|G(s)| dB= 20 log |G(s)|= -20 log (1 +w^2)^ 1/2
Per rappresentare questo modulo in decibel con i diagrammi di Bode basta fare i limiti per alcuni valori di w ben precisi, ad esempio:
lim -20 log (1 +w^2)^ 1/2 = 0
w->0
lim -20 log (1 +w^2)^ 1/2 =00
w->00
lim -20 log (1 +w^2)^ 1/2 = -3 dB
w->1
lim -20 log (1 +w^2)^ 1/2 = -20 dB
w->10
lim -20 log (1 +w^2)^ 1/2 = 0, 04
w->0,1
Riportando il grafico di |G(s)| dB su scala semilogaritmica avremo il grafico di un filtro passa basso con il polo p=1
Calcolo della fase di G(s)=1/(s+1)
Per calcolare la fase di
G(s)=1/(s+1)
ricordiamo che la fase di un numero complesso si ricava con la formula
fase(G(jw))= arctg( Im/Re)
Trasformaiamo quindi la G(s) in G(jw).
Ricordando che s=jw avremo:
G(jw)= 1/(1+jw)
e quindi
fase(Gjw)= - w/1
Il segno meno viene vuori dal fatto che la funzione G(s) ha la variabile s al denominatore.
Calcoliamo quindi i limiti per ricavare il diagramma asistotico;
sono necessari solo tre punti cioè il limite per
w=polo=wp,
w=0
w=00;
possiamo anche calcolare w= 0,1Wp e w=10 wp cioè la decade precedente al polo e la decade successiva al polo.
lim fase G(jw)= lim -arctg w= 0°
w-->0 w-->0
lim fase G(iw) = lim - arctg w= -90°
w-->00 w-->00
lim fase G(jw)= lim - arctg w= -45°
w-->1 w-->1
si possono anche calcolare i limiti della fase di G(jw) nella decade precedente al polo cioè per w=0,1 e per la decade successiva al polo per w=10.
Riportando questi valori nel grafico semilogaritmico in cui in ascisse mettiamo w e in ordinate la sua gase in gradi avremo il diagramma di Bode della fase.
G(s) del filtro passa basso RC
Esercizio: Calcolare la G(s) di un filtro RC e disegnare il suo diagramma del modulo e della fase.
Nel filtro RC si ha una
G(s)= Vu(s)/Vi(s)= (1/Cs)/ ( R+ 1/Cs)= 1/(1+ RC*s) -->
G(S)= 1/(1+RCs)
essendo il polo p della G(s)
p= 1/RC=w
w=2*3.14*f =1 /RC -->
la frequenza di taglio del filtro passa basso è
f=1/( 2*3.14 * RC ) =1/RC
Di solito la costante RC viene chiamata tau (lettere greca) ed ha la dimensione del tempo misurato in seconti cioè
tau= RC=[s]
se il filtro è di tipo RC e
1/RC=[Hz]
Facendo tutti i i limiti della funzione |G(s)|dB , come nell'esercizio precedente), si dimostra che , nel polo p= 1/RC e quindi anche nella frequenza di taglio si ha una attenuazione di - 3dB pari ad una diminuzione del 30% dell'amplificazione ( vedi grafico del diagramma di Bode del modulo in dB).
Il filtro RC e' quindi di tipo passa basso in quanto per pulsazioni inferiori alla pulsazione di taglio si ha |G(s)|dB uguale a zero, dopo la pulsazione di taglio ( o frequenza di taglio), si ha una attenuazione di -20dB/dec, mentre nel polo ( o nella frequenza di taglio) si ha una attenuazione di -3dB ( o del 30%).
Smorzamento per poli complessi coniugati.
Prima Verifica
1) VERIFICA DI
SISTEMI ELETTRONICI AUTOMATICI
CONOSCENZA E COMPRENSIONE:
1) Dare la definizione del teorema della derivata delle trasformate di Laplace..
2) Dare la definizione di trasformata di Laplace e spiegare i motivi per cui è stata introdotta.
3) Spiegare che cosa è un impulso rettangolare e scrivere la sua funzione nel dominio del tempo e nel dominio di s. Cosa è la delta di Dirac?
4) Dire cosa sono i poli e gli zeri di una funzione F(s)= N(s)/ D(s). Spiegarlo con un esempio.
APPLICAZIONI:
5) Dato un filtro CR, disegnare il suo schema elettrico e calcolare la sua funzione di trasferimento nel dominio di s e la sua antitrasformata. Se R = 1 K Ohm e C = 0,1 F quanto vale la sua anti trasformata?
6) Calcolare l’ antitrasformata di Laplace della funzione
F(S)=(s+1)/(s+2)*(s+4)
Utilizzando il metodo dei residui.
Seconda verifica
2) VERIFICA DI
SISTEMI ELETTRONICI AUTOMATICI
CONOSCENZA E COMPRENSIONE
1) Spiegare cosa dice il teorema dell’integrale delle trasformate di Laplace.
2) Dare la definizione del teorema della linearità e fare qualche esempio di un suo utilizzo.
3) Spiegare che cosa è una rampa lineare crescente, disegnare il suo grafico e calcolare la sua funzione nel dominio del tempo e nel dominio di s; e se fosse stata decrescente cosa cambiava?
4) Dire che come vengono trasformati i componenti elementari (resistenze, condensatori e induttori) e le sue tensioni nel dominio di s.
APPLICAZIONI:
5) Dato un filtro RL, disegnare il suo schema elettrico, calcolare la sua funzione di trasferimento nel dominio di s e la sua anti trasformata nel dominio del tempo. Se poniamo R = 1K Ohm ed L = 5 mH quanto vale la sua anti trasformata ?
6 ) Data la seguente funzione
F(s)= s/( s^3 + 4 s^2 + 3 s)
Calcolare la sua anti trasformata applicando il metodo delle derivate.