Metodo Montecarlo
I Metodi Monte Carlo sono un'ampia classe di metodi computazionali basati sul campionamento casuale per ottenere risultati numerici.
Sfruttando uno di questi metodi è possibile generare, con dei numeri casuali, il valore del PI_Greco.
Per calolare il PI_GRECO con il metodo Monte Carlo partiamo dalle seguenti ipotesi:
Sia M un punto di coordinate (x,y) con 0
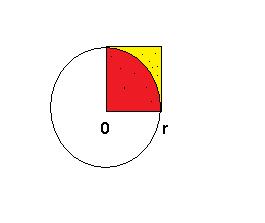
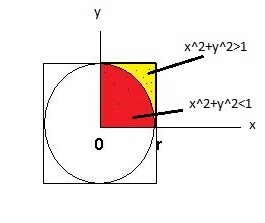
Se x^{2}+y^{2}<1 allora il punto M appartiene al settore di disco (un quarto del cerchio a cui appartiene) di centro (0,0) di raggio 1.
Mentre se il punto è al di fuori del disco si avrà x^{2}+y^{2}>1
L'area di tale disco è il raggio elevato al quadrato per π diviso 4.
Nell'esempio il raggio è pari a uno e quindi l'area di interesse è 1*π/4 = π/4. Il punto può cadere quindi o nel cerchio o nel quadrato circoscritto al cerchio.
La probabilità che il punto cada all'interno del settore di disco è quindi pari al rapporto tra l'area del settore π/4 e l'area del quadrato circoscritto al settore di disco che è 1; quindi la probabilità è π/4.
Facendo il rapporto del numero dei punti che cadono nel settore di disco con il numero dei tiri effettuati si ottiene un'approssimazione del numero π/4 se il numero dei tiri è grande.
Programma in C per il calcolo del PI Greco con il metodo Monte Carlo
In questo programma utiliziamo la funzione
srand(time(NULL));
che genera il seme casuale e la funzione
rand();
che genera il numero casuale.
La funzione srand per poter essere utilizzata ha bisogno dell'inclusione della libreria , time.h; quest la libreria leggerà l'orologio del computer e quindi genererà numeri diversi ogni volta che verrà invocata.
Il metodo Monte Carlo permette di calcolare il numero PI_Greco con la seguente formula
Area_Cerchio/Area_Quadrato=(PI_Greco*raggio*raggio)/(2*raggio)^2= PI_Greco/4
Infatti l'area del cerchio è data dal quadrato del raggio per PI_Greco mentre l'area del quadrato, di lato uguale a due volte il raggio, è data da (2*raggio)^2; il rapporto di queste due aree dà quindi
PI_Greco/4
Facendo la formula inversa si ha che:
PI_Greco=4*(Area_Cerchio)/Area_Quadrato)
La funzione random(time(NULL)): quindi genera dei numeri casuali esterni alla circonferenza e interni al quadrato; se contiamo i punti generati fuori dal cerchio, ma interni al quadrato incrementiamo di uno il numero dei punti all'interno del ciclo for.
Questo avviene con l'istruzione
......
if(x*x+y*y<1) //cioè se il punto è dentro la circonferenza di raggio unitario
++dentro; // incrementa i punti che stanno dentro altrimenti non incrementare
......
dopo il ciclo for calcoliamo il valore di PI_Greco con la formula
PI_Greco=4*(double)dentro/(double)tanti;
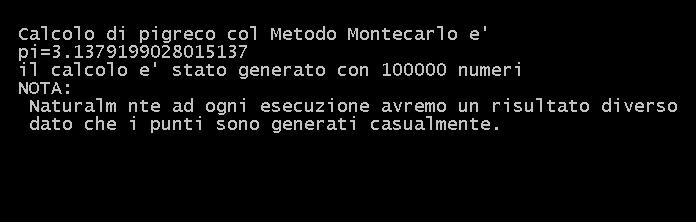
Quando proviamo a lanciare questo programma il valore di PI_Greco è quasi uguale a quello voluto, ma naturalmente si avranno valori diversi per ogni lancio del programma, in quanto il metodo utilizzato è di tipo casuale, cioè random.
Programma completo del metodo Monte Carlo in Dev C
L'output del programma sarà il seguente
Calcoliamo il Pi greco con un foglio a quadretti
IL METODO MONTECARLO PER IL CALCOLO DEL Pi GRECO con un foglio a quadretti
Il metodo Monte Carlo è un metodo probabilistico che ci permette di calcolare il π. Consideriamo una circonferenza di raggio unitario r=1.
Essa avrà un’area pari a
Area del cerchio = r^2*π
Inscriviamo questa circonferenza in un quadrato di lato 2r ed area
Area del quadrato = 2r*2r=4r2
I punti all’interno del quadrato avranno coordinata x e y compresi tra 0 e 1, di questi, quelli che distano meno di 1 dal cerchio cioè quelli che hanno
x^2+y^2<1
si trovano dentro il cerchio, quelli che hanno coordinata
x^2+y^2>1
si trovano fuori dal cerchio e quelli che hanno
x^2+y^2=1
si trovano naturalmente dentro una circonferenza.
Adesso cercherò, attraverso un metodo casalingo, di dimostrare che
da cui ricaviamo che:
π=4* (Area del cerchio/ Area del quadrato)
Prendiamo un foglio di carta con quadretti di 5 mm. Con l’aiuto di un piatto disegniamo un cerchio e lo iscriviamo dentro un quadrato.
Adesso contiamo tutti i quadretti esterni alla circonferenza e che non toccano la circonferenza, e per comodità li indichiamo con un puntino.
In questo modo rispettiamo la regola che i quadretti sono equamente distribuiti sull’intero foglio. Successivamente contiamo tutti i quadretti che intercettano la circonferenza, e tutti i quadretti contenuti nel quadrato.
Ho ottenuto i seguenti valori sperimentali:
N° di punti sui quadretti esterni alla circonferenza = Ne
Ne = 106+111+104+104=425
N° di punti sui quadretti che intersecano la circonferenza=Nc
Nc = 140
N° quadretti totali=Ntot
Ntot = 48*48 = 2304
Punti dentro cerchio= Cmax
Cmax = Ntot-Ne = 2304 – 425=1879
Punti dentro il cerchio escludendo quelli sulla circonferenza= Cmin
Cmin = Ntot-Ne-Nc =2304 - 425 -140 = 1739
Quest’ultima operazione si rende necessaria perché alcuni punti si trovano a metà tra dentro la circonferenza e fuori la circonferenza.
Quindi faccio a media tra i due valori in modo da ottenere i quadretti che mediamente si trovano dentro il cerchio.
Cmedio = (Cmax+Cmin)/2= (1879+1739)/2=1809
Applichiamo adesso la formula per calcolare il :
π = 4*(Area del cerchio / Area del quadrato)
Al posto di Area del cerchio sostituiamo il valore medio dei quadretti che stanno nel cerchio cioè
Cmedio=1809
e al posto dell’area del quadrato inseriamo il numero dei quadretti totali che abbiamo ottenuto
Ntot =2304
Sostituendo abbiamo:
π = 4 * (Cmedio / Ntot)
π =4* (1809/2304 )=3,1406
Ѐ veramente sorprendente, che abbiamo ritrovato il valore del π utilizzando un metodo così semplice, senza l’utilizzo di alcun software. Naturalmente la precisione trovata si ferma solo alla seconda cifra, ma è comunque un buon risultato.