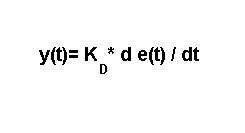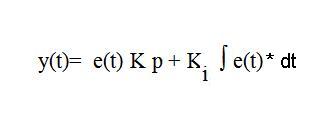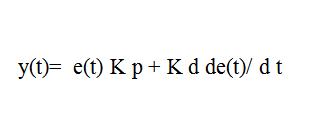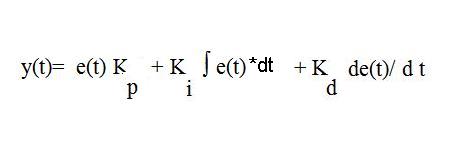Controllare un sistema vuol dire quindi effettuare una regolazione su di esso, regolazione che può essere effettuata con tecniche diverse.
Infatti i sistemi possono essere controllati adottando i seguenti metodi di regolazione:
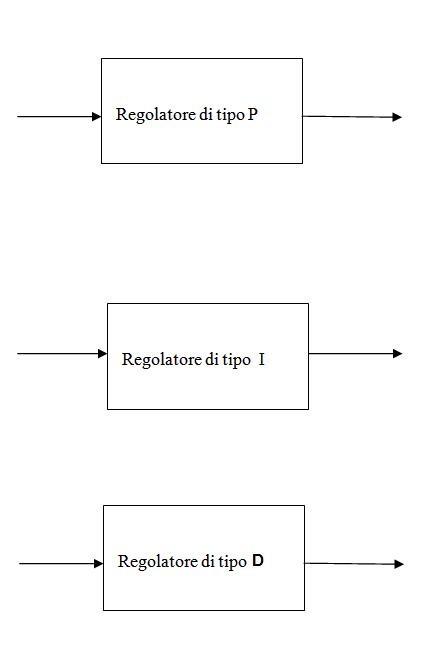
- Regolazone di tipo P o proporzionale
- Regolazione di tipo I o integrativa
- Regolazione di tipo D o derivativa
- Regolazione di tipo PI (proporzionale e integrativa),
- Regolazione PD (proporzionale e derivativa)
- Regolazione PDI (proporzionale-derivativa-integrativa).
Vediamo adesso questi regolatori i loro schemi a blocchi e le loro funzioni di trasferimento nel dominio del tempo e nel dominio di s.
Regolatore di tipo P o Proporzionale
Vediamo adesso il funzionamento di un regolatore di tipo P o proporzionale.
Un amplificatore operazionale che ha un guadagno A= K con K= costante è un regolatore di tipo P.
Il Guadagno A può essere:
A= 1 --> circuito in configurazione buffer non invertente con guadagno unitario
A>1 --> circuito in configurazione amplificatore non invertente o non invertente se consideriamo il modulo di A;
A<1--> il circuito è un filtro con guadagno minore di 1
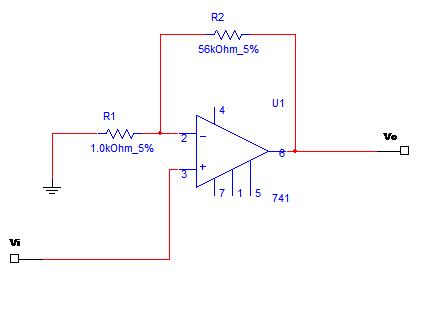
Regolatore di tipo P con A.O. non invertente
CIRCUITI CON AMPLIFICATORI OPERAZIONALI:
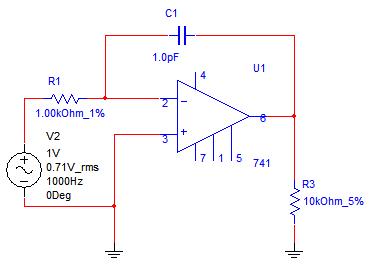
Consiseriamo un A.O. in configurazione non invertente e inviamo il segnale dal morsetto non invertente; retroazioniamo l'amplificatore con le due resistenze R1 e R2 collegate come nelle figura precedente. In questo caso la tensione di uscita prelevata dal pin 6 fino alla massa farà circolare sulle due resistenze una corrente I. Per la legge di Ohm sarà:
Vu= I* (R1+R2) -->
I=Vu/(R1+R2)
Per il principio di massa virtuale sul morsetto non invertente ( pin 2) si avrà una tensione V+ circa uguale a Vi. Questa tensione farà circolare sulla resistenza R1 una corrente I pari a
I=V+/R1= Vi/R1 -->
I= Vi/R1
ugualiando le due I così trovate avremo:
Vi/R1=Vu/(R1+R2) --> Vu/Vi= (R1+R2)/R1 -->
Vu/Vi= 1+ R2/R1
Quest'ultima formula ci dice che l'amplificato re operazionale amplifica in modo non invertente ed ha un guadagno
A= 1+R2/R1
In questo caso
A=1+R2/R1= K
e quindi l'amplificatore operazionale è un regolatore di tipo P.
Regolatore di tipo I ad A.O. o Integratore ideale
In questo regolatore ad amplificatore operazionale, in uscita si ha l'integrale del segnale di ingresso.
Regolatore di tipo I
Un regolatore di tipo I ad amplificatore operazionale può essere realizzato sostituendo la resistenza R2 dell'amplificatore in configurazione invertente con un condensatore.
G(s)= - Z2/Z1= -(1/Cs)/R1 = - 1/(CR1 s)
--> Vu(s)= G(s) *Vi(s)= (-1/(CR1s))* Vi(s)
In questo caso:
la G(s) ha un polo nullo che per w-->0 porta il suo modulo ad +oo
Infatti il
lim w-->0 |G(s)| dB=lim w-->0 20 log|1/(CR1 s)= lim w-->0 -20log|CR1 s| = +oo
mentre il limite per w che tende ad infinito porta il suo modulo in decibel a meno infinito.
Questo fa si che il regolatore di tipo I ideale è molto instabile cioè porta il nostro amplificatore alla saturazione.
In sua vece, per motivi pratici, si utilizza il regolatore PI che ha in parallelo al condensatore una resistenza R2 che abbassa il suo guadagno.
In questo caso quindi la G(s) ha un polo nullo e quindi il suo diagramma di Bode avrà l'andamento di una linea retta inclinata ma con una pendenza di -20dB/dec.
Matematicamente il circito integratore, nel dominio del tempo, fa l'integrale del segnale di ingresso, che abbiamo chiamato e(t)
Regolatore D
Il regolatore D invece al posto della Z1 ha un condensatore e al poeto della Z2 ha una resistenza.
La sua G(s) è:
G(s) = - Z2/Z1 = - R2/(1/Cs) = - R2C*s
--> Vu(s)= G(s)*Vi(s)
--> Vu(s)= (-R2 C*s)*Vi(s)
|G(s)|dB= 20 log |R2Cs|
In questo caso quindi la G(s) ha uno zero nullo e quindi il suo diagramma di Bode avrà l'andamento di una linea retta inclinata ma con una pendenza di 20dB/dec.
Matematicamente il circuito regolatore fa la derivata del segnale di ingresso:
vu(t)= - R2 C d vi(t)/dt
posto
Vi (t)= e(t) cioè segnale di errore nel dominio del tempo, si ha:
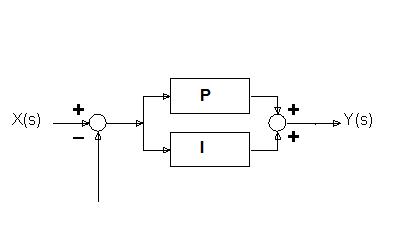
Schemi a blocchi dei regolatori PI
Schema elettrico di un regolatore PI ad Amplificatore Operazionale
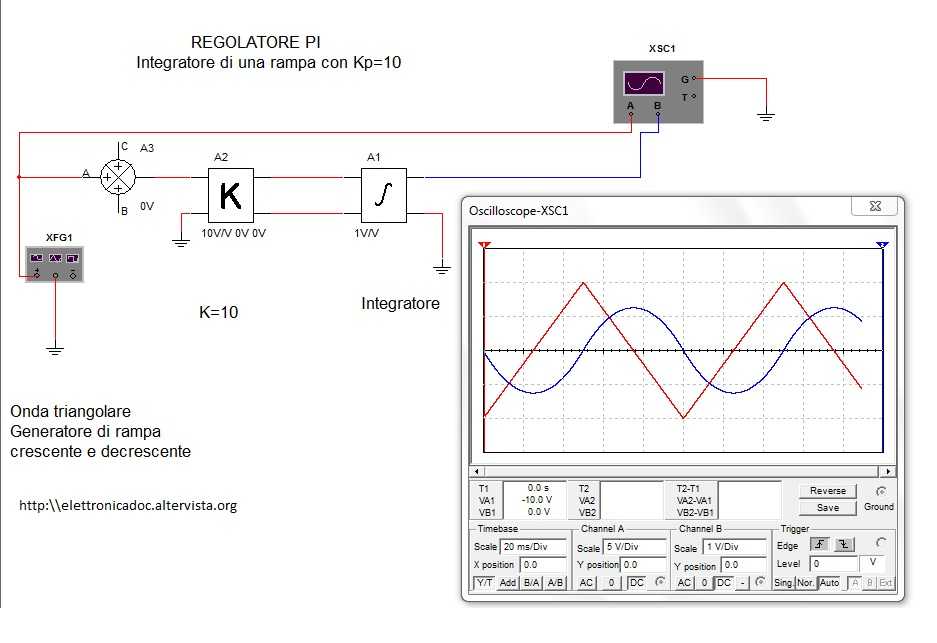
Regolatore PI: schema a blocchi con Multisim
Inviamo in ingresso un segnale triangolare
Realizziamo adesso la simulazione con il Multisim di un REGOLATORE PI realizzato attraverso un blocco K=10 e un blocco integratore I. All'ingresso del blocco K viene inserito una rampa crescente e una rampa decrescente con lìinvio di un'onda triangolare di frequenza f=10 Hz.
Alluscita del blocco integratore si otterrà la ricostruzione di un'onda di tipo sinusoidale.
Cioè l'integrale di un'onda triangolare è un'onda sinusoidale,
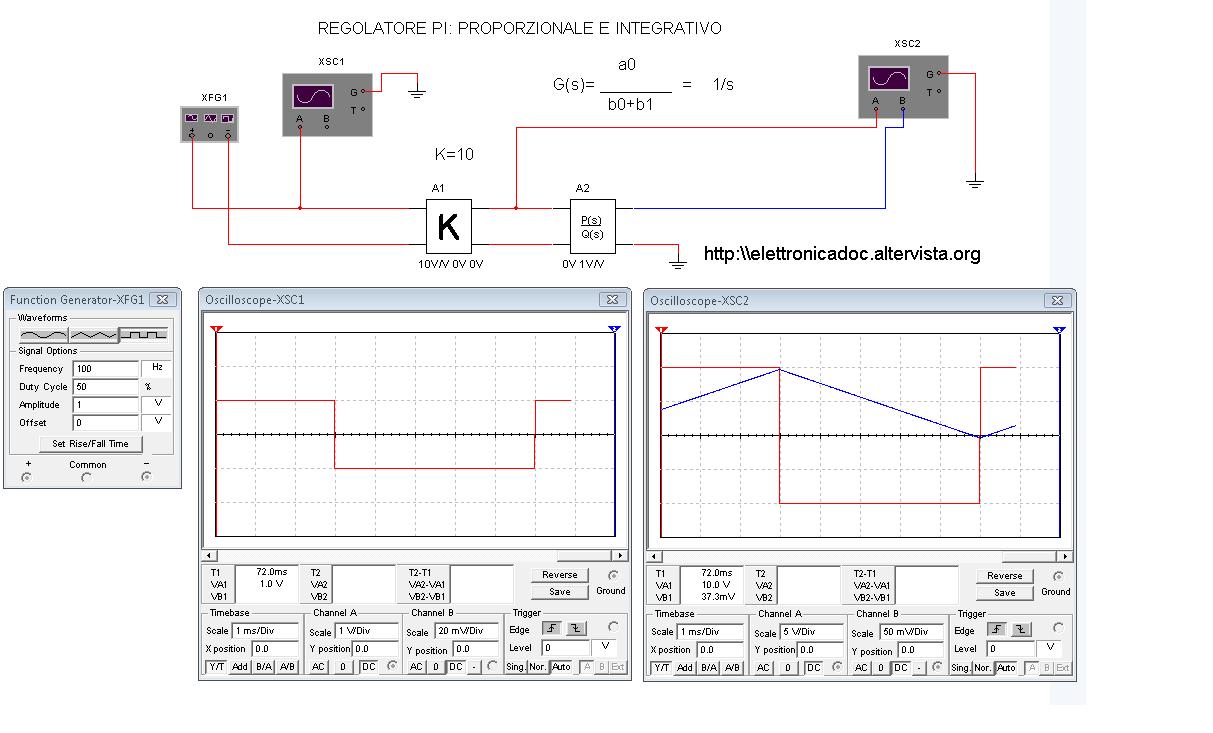
Simulazione con multisim di un regolatore PI con in ingresso un'onda quadra
Realizziamo adesso la simulazione del regolatore PI con il software Multisim.
Inviamo al regolatore un'onda quadra di ampiezza 1V con una frequenza f=100Hz all'ingresso del blocco proporzionale che ha K=10 .
All'uscita del blocco K si avrà sempre un'onda quadra ma di ampiezza 10 V.
Questo segnale lo inviamo all'ingresso dell'integratore, che dà in uscita una rampa crescente o decrescente a seconda che il gradino è positivo o negativo.
L'ampiezza della rampa terminerà molto velocemente al sopraggiungere del gradino di segno opposto.
Questo si può vedere nella seguente simulazione fatta con il software Multisim in cui si vede che l'ampiezza massima della rampa vale 100mV, cioè due quadrettini dell'oscilloscopio che ha una scala V= 50mV per ogni quadrettino).
Regolatore PD
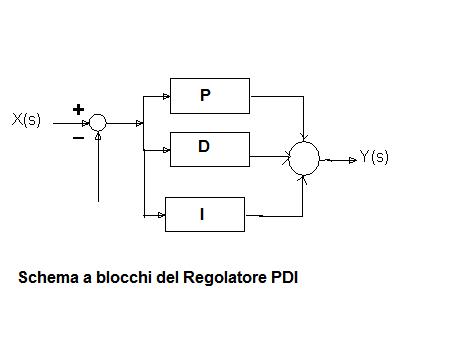
Regolatore PDI
Nei regolatori PDI abbiamo i tre blocchi con costante proporzionale Kp, costante integrativa Ki e costante derivativa Kd che si sommano tra di loro e che ha questo schema a blocchi.
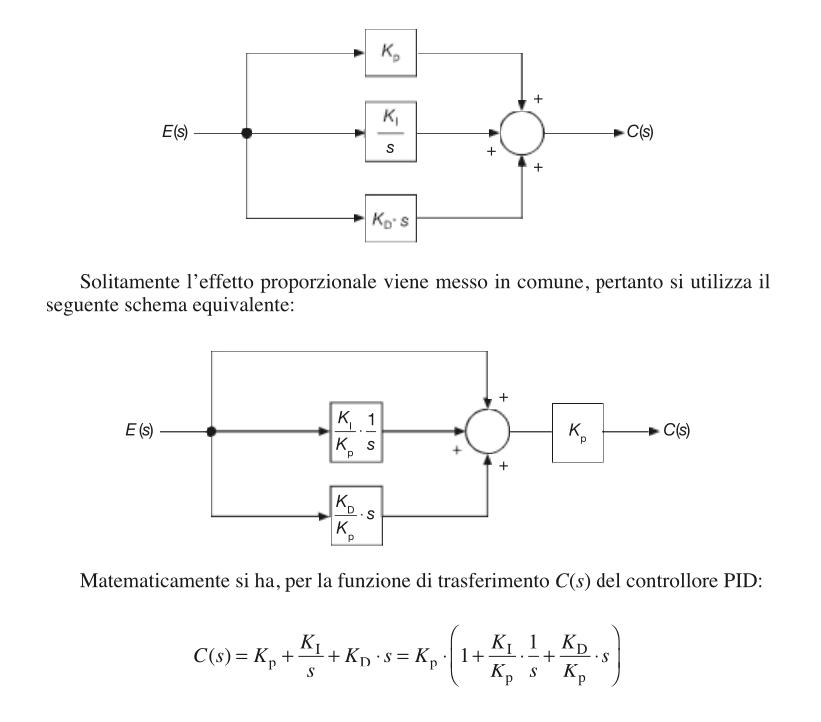
In alcuni testi scolastici il segnale di ingresso del regolatore PDI è anche chiamato E(s) cioè segnale di errore, e il segnali di uscita del regolatore PDI con il nome C(s) cioè segnale controllante. Utilizzando questa simbologia si ha il seguente schema a blocchi:
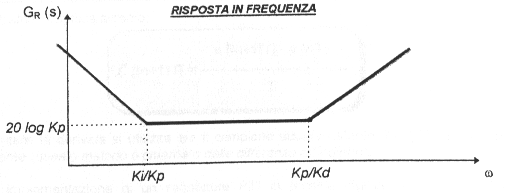
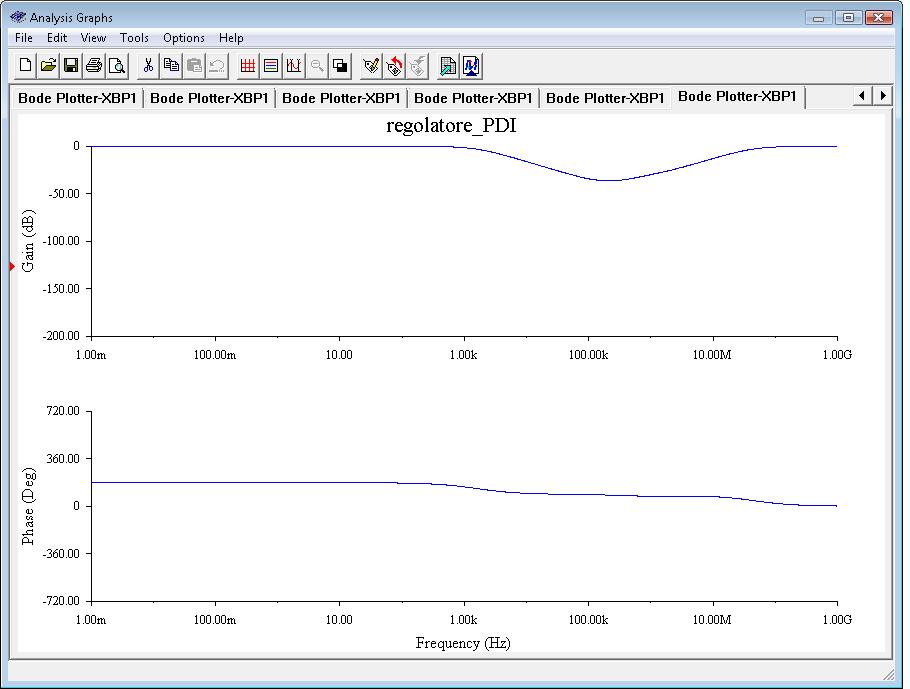
Questo regolatore ha una risposta in frequenza data dalla somma dei tre contributi: proporzionale, derivativo e integratico e il suo diagramma di Bode è il seguente:
La stessa formula nel dominio del tempo si scrive: